
分析 ①,由 sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)$≤\sqrt{2}$;不可能;
②举反例:α=4200,β=100是第一象限角,且α>β,则cosα>cosβ;
③函数y=sin2x的图象向左平移$\frac{π}{4}$个单位,得到函数y=2sin2(x+$\frac{π}{4}$)的图象;
④定义在R上的奇函数f(x)满足f(x+2)=f(-x)⇒f(x+2)=f(-x)=-f(x)⇒f(x+4)=f(x)⇒周期T=4;则f(2015)=f(3)=f(-1).
解答 解:对于①,由 sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)$≤\sqrt{2}$;不可能,故错;
对于②,举反例:α=4200,β=100是第一象限角,且α>β,则cosα>cosβ,故错;
对于③,函数y=sin2x的图象向左平移$\frac{π}{4}$个单位,得到函数y=2sin2(x+$\frac{π}{4}$)的图象,故错;
对于④,定义在R上的奇函数f(x)满足f(x+2)=f(-x)⇒f(x+2)=f(-x)=-f(x)⇒f(x+4)=f(x)⇒周期T=4;则f(2015)=f(3)=f(-1)=-f(1)=-2,故正确.
故答案:④.
点评 本题考查了命题的真假判定,涉及到了三角函数的概念及性质,属于中档题.


科目:高中数学 来源: 题型:填空题
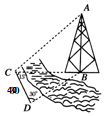 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.测得∠BCD=15°,∠BDC=30°,CD=40米,并在点C测得塔顶A的仰角为60°,则塔高AB=20$\sqrt{6}$米.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.测得∠BCD=15°,∠BDC=30°,CD=40米,并在点C测得塔顶A的仰角为60°,则塔高AB=20$\sqrt{6}$米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $\frac{3}{2}$ | C. | 3 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | [-2,2] | C. | (-2,2] | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com