
| 性别 是否需要志愿者 | 男 | 女 | 总计 |
| 需要 | 30 | ||
| 不需要 | 160 | ||
| 总计 | 200 | 500 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
分析 (Ⅰ)根据题意,计算表中缺少的数据,填写2×2列联表,
再根据表中数据计算需要帮助的老年人比例估计值;
(Ⅱ)根据表中数据,计算观测值,由此得出概率结论.
解答 解:(Ⅰ)根据题意,计算表中缺少的数据,填写2×2列联表如下:
| 性别 是否需要志愿者 | 男 | 女 | 总计 |
| 需要 | 40 | 30 | 70 |
| 不需要 | 160 | 270 | 430 |
| 总计 | 200 | 300 | 500 |
点评 本题考查了2×2列联表以及独立性检验的应用问题,也考查了概率模型的应用问题,是基础题目.


科目:高中数学 来源: 题型:填空题
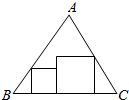 从等边三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=3+$\sqrt{3}$,则这两个正方形的面积之和的最小值为$\frac{9}{2}$.
从等边三角形纸片ABC上,剪下如图所示的两个正方形,其中BC=3+$\sqrt{3}$,则这两个正方形的面积之和的最小值为$\frac{9}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )
某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )| A. | 20 | B. | 22.5 | C. | 22.75 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
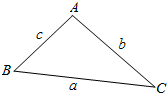 (1)如图所示.在△ABC中,射影定理可表示为a=b•cosC+c•cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.
(1)如图所示.在△ABC中,射影定理可表示为a=b•cosC+c•cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com