
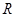 上的函数
上的函数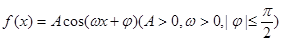 ,最大值与最小值的差为4,相邻两个最低点之间距离为
,最大值与最小值的差为4,相邻两个最低点之间距离为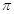 ,函数
,函数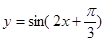 图象所有对称中心都在
图象所有对称中心都在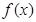 图象的对称轴上.
图象的对称轴上.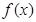 的表达式;
的表达式;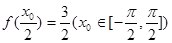 ,求
,求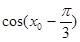 的值;
的值;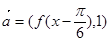 ,
,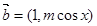 ,
,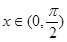 ,若
,若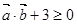 恒成立,求实数
恒成立,求实数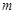 的取值范围.
的取值范围.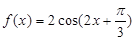 (2)
(2)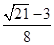 (3)
(3)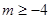
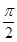 ),最大值与最小值的差为4,相邻两个最低点之间距离为π,我们易计算出A值,及最小正周期,进而求出ω值,再由函数
),最大值与最小值的差为4,相邻两个最低点之间距离为π,我们易计算出A值,及最小正周期,进而求出ω值,再由函数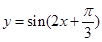 图象所有的对称中心都在y=f(x)图象的对称轴上,求出φ值,即可得到f(x)的表达式;
图象所有的对称中心都在y=f(x)图象的对称轴上,求出φ值,即可得到f(x)的表达式;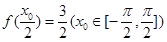 ,结合(1)中所求的函数解析式,可得
,结合(1)中所求的函数解析式,可得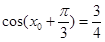 ,
,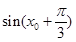 的值,然后根据两角差的余弦公式,即可求出答案.
的值,然后根据两角差的余弦公式,即可求出答案.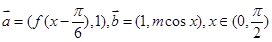 ,
,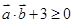 恒成立,可以转化为函数恒成立问题,构造函数,求出其最值,即可得到答案.
恒成立,可以转化为函数恒成立问题,构造函数,求出其最值,即可得到答案.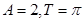 ,
,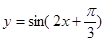 与f(x)相差
与f(x)相差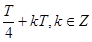 ,即相差
,即相差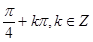 ,
,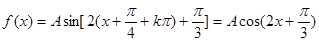 或
或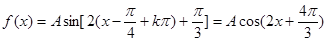 (舍),
(舍),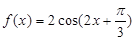 . ……………………4分
. ……………………4分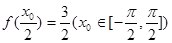 ,即
,即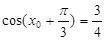 ,
,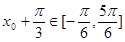 ,又
,又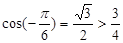 ,y=cosx在
,y=cosx在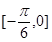 单调递增,
单调递增,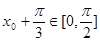 ,所以
,所以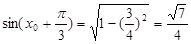 ,
,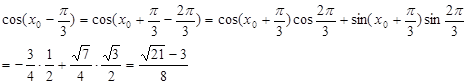 ………9分
………9分 ,
, ,
,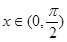
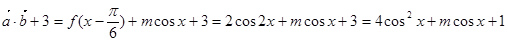 ,
,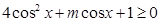 ,得
,得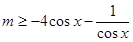 对于
对于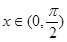 恒成立,
恒成立, ,故
,故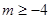 . ………………14分
. ………………14分

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com