
△ABC的内角A、B、C的对边分别为a,b,c,已知a=bcosC+csinB。
(1)求B;
(2)若b=2,求△ABC面积的最大值。
(1)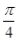
(2)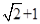
【解析】(1)由题意及正弦定理得sinA=sinBcosC+sinCsinB ①
又A=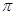 -(B+C),所以sinA=sin(B+C)=sinBcosC+cosBsinC ②
-(B+C),所以sinA=sin(B+C)=sinBcosC+cosBsinC ②
由①和②得 sinBcosC+sinCsinB= sinBcosC+cosBsinC  sinCsinB=cosBsinC
sinCsinB=cosBsinC
又C为△ABC的内角,所以sinC≠0, 所以sinB=cosB,即B=
(2)∵△ABC的面积S=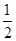 acsinB=
acsinB=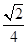 ac
ac
由题意及余弦定理得4=a2+c2-2accos
 a2+c2=4+
a2+c2=4+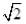 ac
ac
又a2+c2≥2ac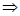 4+
4+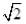 ac≥2ac
ac≥2ac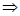 ac≤
ac≤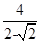 等号当且仅当a=c时成立
等号当且仅当a=c时成立
∴S=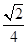 ac≤
ac≤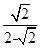 =
=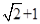
因此△ABC面积的最大值为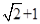


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014高考名师推荐数学理科矩阵与变换(解析版) 题型:解答题
设矩阵M= (其中a>0,b>0).
(其中a>0,b>0).
(1)若a=2,b=3,求矩阵M的逆矩阵M-1;
(2)若曲线C:x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C’: ,求a,b的值.
,求a,b的值.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科正态分布(解析版) 题型:选择题
已知随机变量 服从正态分布N(2,σ2),且P(
服从正态分布N(2,σ2),且P( <4)=0.8,则P(0<
<4)=0.8,则P(0< <2)=( )
<2)=( )
A.0.6 B.0.4 C.0.3 D.0.2
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科正弦定理(解析版) 题型:选择题
已知角B为钝角的△ABC的内角A、B、C所对应边分别为a,b,c,若a=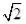 c,cosC=
c,cosC=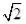 sinA,则cosB= ( )
sinA,则cosB= ( )
A. -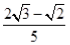
B. -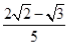
C. -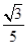
D. -
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科椭圆(解析版) 题型:解答题
已知点 ,圆C:
,圆C: 与椭圆E:
与椭圆E: 有一个公共点
有一个公共点 ,
, 分别是椭圆的左、右焦点,直线
分别是椭圆的左、右焦点,直线 与圆C相切.
与圆C相切.

(1)求m的值与椭圆E的方程;
(2)设Q为椭圆E上的一个动点,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科数列的概念、等差数列、等比数列(解析版) 题型:解答题
设数列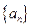 的前
的前 项和为
项和为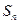 .已知
.已知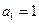 ,
,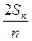 =an+1-
=an+1-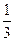 n2-n-
n2-n-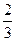 (
( )
)
(1) 求 的值;
的值;
(2) 求数列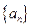 的通项公式;
的通项公式;
(3) 证明:对一切正整数 ,有
,有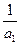 +
+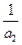 +…+
+…+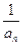 <
<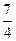 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com