练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知角B为钝角的△ABC的内角A、B、C所对应边分别为a,b,c,若a=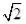c,cosC=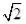sinA，则cosB=   (    )

    A. -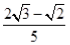

    B. -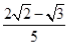

    C. -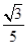

    D. -

     

    A

    【解析】∵a=c,由正弦定理知,sinA=sinC

    ∴cosC=sinA=2sinCtanC=

    ∵cos2C= =且角C为锐角

    ∴cosC=sinC=,

    sinA=sinC =cosA=

    ∵cosB=-cos(A+B)=-(cosAcosC-sinAsinC)

    ∴cosB=-(×-×)=-

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014高考名师推荐数学理科线性规划（解析版） 题型：选择题

    设关于x，y的不等式组表示的平面区域内存在点，满足．求得m的取值范围是(　　)

    A．(－∞，)

    B．(－∞，)

    C．(－∞，)

    D．(－∞，)

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科积分（解析版） 题型：解答题

    已知函数．

    （1）讨论f(x)在区间（0，1）上的单调性；

    （2）当a∈[3，+∞)时，曲线上总存在相异的两点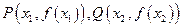，使得曲线在点P，Q处的切线互相平行，求证：．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科正态分布（解析版） 题型：解答题

    根据以往的经验，某工程施工期间的降水量X（单位：mm）对工期的影响如下表：

    降水量X

    工期延误天数

    0

    2

    6

    10

    历年气象资料表明，该工程施工期间降水量X小于300，700，900的概率分别为0．3，0．7，0．9． 求：

    （1）工期延误天数的均值与方差；（2）在降水量X至少是300的条件下，工期延误不超过6天的概率．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科正弦定理（解析版） 题型：解答题

    △ABC的内角A、B、C的对边分别为a，b，c，已知a=bcosC+csinB。

    （1）求B；

    （2）若b=2，求△ABC面积的最大值。

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科椭圆（解析版） 题型：解答题

    已知椭圆的离心率，连接椭圆的四个顶点得到的菱形的面积为4．

    (1)求椭圆的方程；

    (2)设直线与椭圆相交于不同的两点，已知点的坐标为，点在线段的垂直平分线上，且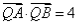，求的值.

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科椭圆（解析版） 题型：填空题

    已知椭圆C:的左焦点为F，C与过原点的直线相交于A，B两点，连接AF，BF，若，则C的离心率e=         ．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科数列的概念、等差数列、等比数列（解析版） 题型：填空题

    互不相同的点A1，A2，…，An，…和B1，B2，…，Bn，…分别在角O的两条边上OA和OB上，所有AnBn相互平行，且所有梯形AnBnBn+1An+1的面积均相等．设OAn=an若a1=1，a2=2则数列{an}的通项公式是_________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科抛物线（解析版） 题型：解答题

    已知直线l：y=x+m，m∈R．

    (1)若以点M（2，0）为圆心的圆与直线l相切与点P，且点P在y轴上，求该圆的方程；

    (2)若直线l关于x轴对称的直线为lˊ，问直线lˊ与抛物线C：是否相切？说明理由．

     

    查看答案和解析>>

    同步练习册答案