
已知直线l:y=x+m,m∈R.
(1)若以点M(2,0)为圆心的圆与直线l相切与点P,且点P在y轴上,求该圆的方程;
(2)若直线l关于x轴对称的直线为lˊ,问直线lˊ与抛物线C: 是否相切?说明理由.
是否相切?说明理由.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014高考名师推荐数学理科正弦定理(解析版) 题型:选择题
已知角B为钝角的△ABC的内角A、B、C所对应边分别为a,b,c,若a=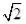 c,cosC=
c,cosC=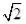 sinA,则cosB= ( )
sinA,则cosB= ( )
A. -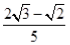
B. -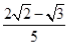
C. -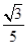
D. -
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科数列的概念、等差数列、等比数列(解析版) 题型:选择题
若等比数列{an}满足a2+a4=20,a3+a5=40,前100项和S100=( )
A.2101
B.2101+2
C.2100-2
D.2100
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科排列组合综合应用(解析版) 题型:选择题
一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的坐法种数为( )
A.3×3!
B.
C.
D.9!
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科抛物线(解析版) 题型:选择题
已知抛物线C: 的焦点为F,直线y=2x-4与C交于A,B两点.则cos∠AFB=( )
的焦点为F,直线y=2x-4与C交于A,B两点.则cos∠AFB=( )
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科平面向量坐标运算 数量积的定义(解析版) 题型:解答题
已知向量 ,设函数
,设函数 .
.
(1)求f(x)的最小正周期;
(2)求f(x)在[0, ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科双曲线(解析版) 题型:选择题
已知中心在原点的双曲线C的右焦点为F(3,0),离心率等于 ,在双曲线C的方程是( )
,在双曲线C的方程是( )
A. B.
B.
C.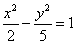 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com