练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知向量，设函数．

    (1)求f(x)的最小正周期;

    (2)求f(x)在[0，]上的最大值和最小值．

     

    (1)π

    (2)最大值是1，最小值是－

    【解析】(1)f(x)=a·b=(cosx，－)·(sinx，cos2x)

    =cosxsinx－cos2x=sin2x－cos2x=sin(2x－)

    f(x)的最小正周期为T=π，

    (2)∵0≤x≤，

    ∴－≤2x－≤．由正弦函数的性质知，sin(2x－)∈[－，1]

    当2x－=，即x=时，f(x)取得最大值1．

    当2x－=－，即x=0时，f(0)=－，

    因此， f(x)在[0，]上的最大值是1，最小值是－．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014高考名师推荐数学理科椭圆（解析版） 题型：填空题

    已知椭圆C:的左焦点为F，C与过原点的直线相交于A，B两点，连接AF，BF，若，则C的离心率e=         ．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科排列组合综合应用（解析版） 题型：选择题

    如图，用四种不同颜色给图中的A，B，C，D，E，F六个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同颜色，则不同的涂色方法有（    ）

    A．288种

    B．264种

    C．240种

    D．168种

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科抛物线（解析版） 题型：解答题

    已知直线l：y=x+m，m∈R．

    (1)若以点M（2，0）为圆心的圆与直线l相切与点P，且点P在y轴上，求该圆的方程；

    (2)若直线l关于x轴对称的直线为lˊ，问直线lˊ与抛物线C：是否相切？说明理由．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科抛物线（解析版） 题型：选择题

    已知点P是抛物线y2=2x上的动点，点P到准线的距离为d，且点P在y轴上的射影是M，点A(，4)，则|PA|+|PM|的最小值是

    A．

    B．4

    C．

    D．5

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科平面向量坐标运算 数量积的定义（解析版） 题型：填空题

    在平行四边形ABCD中，∠A=，边AB、AD的长分别为2、1，若N、N分别是边BC、CD上的点，且满足=，则的取值范围是          。

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科平面向量坐标运算 数量积的定义（解析版） 题型：选择题

    在平面直角坐标系中，O(0，0)，P(6，8)，将向量按逆时针旋转后，得向量，则点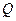的坐标是（    ）

    A．

    B．

    C．

    D．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科复数的加减复数的乘除和乘方（解析版） 题型：选择题

    已知复数z1满足(z1－2)(1＋i)＝1－i(i为虚数单位)，复数z2的虚部为2，且z1·z2是实数，则z2=(   )

    A. 4-2i

    B. 4+2i

    C. 2+4i

    D. 2-4i

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科利用导数求最值和极值（解析版） 题型：选择题

    函数f(x)的定义域为R，f(－1)=2，对任意x∈R，f′(x)＞2，则f(x)＞2x+4的解集为(    )

    A．(－1，1)

    B．(－1，+∞)

    C．(－∞，－1)

    D．(－∞，+∞)

     

    查看答案和解析>>

    同步练习册答案