
| A. | 0<r≤$\sqrt{2}$ | B. | 1<r<$\sqrt{2}$ | C. | 1<r≤$\sqrt{2}$ | D. | r>$\sqrt{2}$ |
分析 将直线方程代入圆的方程得:(m2+1)x2+2mx+1-r2=0,根据韦达定理有则x1+x2=$\frac{-2m}{{m}^{2}+1}$,x1x2=$\frac{1-{r}^{2}}{{m}^{2}+1}$;可根据题意转化为:(1+m2)x1x2+m(x1+x2)+1≥0,即r2≤$\frac{2}{{m}^{2}+1}$有解.
解答 解:将直线方程代入圆的方程得:(m2+1)x2+2mx+1-r2=0,
△=4m2-4(m2+1)(1-r2)>0得r2>$\frac{1}{{m}^{2}+1}$恒成立,即r>1.
设点A(x1,y1),B(x2,y2),则x1+x2=$\frac{-2m}{{m}^{2}+1}$,x1x2=$\frac{1-{r}^{2}}{{m}^{2}+1}$,
|$\overrightarrow{OA}$+$\overrightarrow{OB}$|≥|$\overrightarrow{AB}$|即|$\overrightarrow{OA}$+$\overrightarrow{OB}$|≥|$\overrightarrow{OB}$-$\overrightarrow{OA}$|,平方得$\overrightarrow{OA}$•$\overrightarrow{OB}$≥0,即x1x2+y1y2≥0,
即x1x2+(mx1+1)(mx2+1)≥0,即(1+m2)x1x2+m(x1+x2)+1≥0,
即r2≤$\frac{2}{{m}^{2}+1}$有解,即r2≤2,即r≤$\sqrt{2}$
综合知:1<r≤$\sqrt{2}$
故选:C
点评 本题主要考查了直线与圆的联立方程组,向量加法基础以及转化思想的应用,属中等题.


科目:高中数学 来源: 题型:解答题
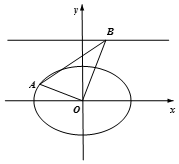 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),离心率为$\frac{{\sqrt{2}}}{2}$,左准线方程是x=-2,设O为原点,点A在椭圆C上,点B在直线y=2上,且OA⊥OB.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),离心率为$\frac{{\sqrt{2}}}{2}$,左准线方程是x=-2,设O为原点,点A在椭圆C上,点B在直线y=2上,且OA⊥OB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com