
分析 使得原函数有意义,便有1-x2+a≥0,从而x2≤1+a,并且可得到$0≤f(x)≤\sqrt{1+a}$,需讨论a是否为-1:a=-1时,可以验证符合条件B⊆A;而a>-1时,会得到$A=[-\sqrt{1+a},\sqrt{1+a}]$,B=[0,$\sqrt{1+a}$],从而看出满足B⊆A,这样即可得出实数a的取值范围.
解答 解:使原函数有意义,则:(1-x2)+a≥0;
∴x2≤1+a (1);
又1-x2≤1,∴(1-x2)+a≤1+a;
∴$0≤\sqrt{(1-{x}^{2})+a}≤\sqrt{1+a}$;
(1)若a=-1,则A=B={0},满足B⊆A;
(2)若a>-1,则B=[0,$\sqrt{1+a}$];
解不等式(1)得,$-\sqrt{1+a}≤x≤\sqrt{1+a}$;
∴$A=[-\sqrt{1+a},\sqrt{1+a}]$;
显然满足B⊆A;
∴综上得,实数a的取值范围为[-1,+∞).
故答案为:[-1,+∞).
点评 考查函数定义域、值域的概念,及求法,一元二次不等式的解法,根据不等式的性质的性质求函数的值域,以及子集的概念.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016-2017学年河北涞水波峰中学高一9月月考数学试卷(解析版) 题型:解答题
经市场调查,某门市部的一种小商品在过去的20天内的日销售量(件)与价格(元)均为时间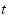 (天)的函数,且日销售量近似满足函数
(天)的函数,且日销售量近似满足函数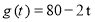 (件),而且销售价格近似满足于
(件),而且销售价格近似满足于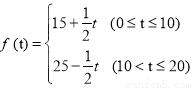 (元).
(元).
(1)试写出该种商品的日销售额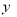 与时间
与时间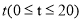 的函数表达式;
的函数表达式;
(2)求该种商品的日销售额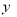 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36 | B. | 37 | C. | 38 | D. | 39 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com