
(1)若P1、P2点的横坐标分别为x1、x2,则x1、x2之间满足怎样的关系?并证明你结论;
(2)求双曲线E的方程;
(3)设双曲线E上的动点M,两焦点为F1,F2,若MF1与MF2的夹角为钝角,求M点横坐标x0的取值范围.

解:(1)由e2=![]() =1+(
=1+(![]() )2=(
)2=(![]() )2,得
)2,得![]() =
=![]() .
.
∴两渐近线OP1、OP2的方程分别为y=![]() x和y=-
x和y=-![]() x.
x.
设点P1(x1,![]() x1)、点P2(x2,-
x1)、点P2(x2,-![]() x).
x).
设∠P1OP2=2α,则tanα=![]() ,∴sin2α=
,∴sin2α=![]()
cos2α=![]()
又S△OP1P2=![]() |
|![]() ||
||![]() |sin2α=
|sin2α=![]() ·|
·|![]() ||
||![]() |=
|=![]() ,
,
∴|![]() ||
||![]() |=
|=![]() .
.
∴![]() ·
·![]() =|
=|![]() ||
||![]() |cos2α=
|cos2α=![]() ×(
×(![]() )=
)=![]() =x1x2
=x1x2![]() x1x2=
x1x2=![]() ·x1x2,即x1x2=
·x1x2,即x1x2=![]() .
.
(2)由点P为线段![]() 的一个三等分点可知,点P分
的一个三等分点可知,点P分![]() 所成的比λ=2,
所成的比λ=2,
∴P点坐标为(![]() ),即(
),即(![]() ).
).
设P(x,y),则x=![]() 且y=
且y=![]() ,即x1+2x2=3x且x1-2x2=2y,
,即x1+2x2=3x且x1-2x2=2y,
∴(3x)2-(2y)2=(x1+2x2)2-(x1-2x2)2=8x1x2=36,即![]() =1.
=1.
(3)由(2)知c=![]() ,∴F1(
,∴F1(![]() ,0),
,0),
F2(![]() ,0),y02=
,0),y02=![]() -9,
-9,
∴![]() ·
·![]() =|
=|![]() ||
||![]() |cos<
|cos<![]() ,
,![]() >=(
>=(![]() -x0,-y0)·(
-x0,-y0)·(![]() -x0,-y0)=x02-13+y02=x02-13+
-x0,-y0)=x02-13+y02=x02-13+![]() -9=
-9=![]() -22<0,即|x0|<
-22<0,即|x0|<![]() .
.
又|x0|>2,
故x0的取值范围为(-![]() ,-2)∪(2,
,-2)∪(2,![]() ).
).


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| F1A |
| F2A |
| π |
| 3 |
| 2π |
| 3 |
4
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•荆门模拟)如图,已知直线OP1,OP2为双曲线E:
(2013•荆门模拟)如图,已知直线OP1,OP2为双曲线E:| x2 |
| a2 |
| y2 |
| b2 |
| 27 |
| 4 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省荆门市高三元月调考文科数学试卷(解析版) 题型:解答题
(本小题满分14分)如图,已知直线OP1,OP2为双曲线E: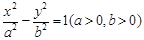 的渐近线,△P1OP2的面积为
的渐近线,△P1OP2的面积为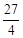 ,在双曲线E上存在点P为线段P1P2的一个三等分点,且双曲线E的离心率为
,在双曲线E上存在点P为线段P1P2的一个三等分点,且双曲线E的离心率为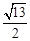 .
.
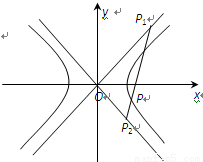
(1)若P1、P2点的横坐标分别为x1、x2,则x1、x2之间满足怎样的关系?并证明你的结论;
(2)求双曲线E的方程;
(3)设双曲线E上的动点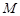 ,两焦点
,两焦点 ,若
,若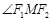 为钝角,求
为钝角,求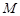 点横坐标
点横坐标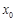 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com