
分析 (1)求导,对a分类讨论,利用导数即可得出其单调性;
(2)由题意,将原式转化成2a-1≥b2a-1恒成立,换元将2a-1=t∈[2,m],构造辅助函数$\frac{lnt}{t}$=g(t),求导,根据导数求得函数的单调区间,由函数g(2)=g(4),对m分类讨论,根据对数函数的运算现在求得b的取值范围.
解答 解:(1)f′(x)=(ax2-x)ex=x(ax-1)ex.
当a=0,则f′(x)=-xex,令f′(x)>0,则x<0,令f′(x)<0,则x>0;
若a<0,由f′(x)>0,解得:$\frac{1}{a}$<x<0,f′(x)<0,解得:x>0或x<$\frac{1}{a}$,
若a>0,由f′(x)>0,解得:0<x<$\frac{1}{a}$,f′(x)<0,解得:x>$\frac{1}{a}$或x<0,
综上可得:
当a=0时,函数f(x)的增区间为(-∞,0),减区间为(0,+∞);
当a<0时,函数f(x)的增区间为($\frac{1}{a}$,0),减区间为(0,+∞),(-∞,$\frac{1}{a}$);
当a>0时,函数f(x)的增区间为($\frac{1}{a}$,+∞),(-∞,0),减区间为(0,$\frac{1}{a}$);
(2)f(x)≥b2a-1${e}^{\frac{1}{a}}$恒成立,f($\frac{1}{a}$)≥b2a-1${e}^{\frac{1}{a}}$恒成立,
∴$\frac{1}{{e}^{a}}(2a-1)$≥b2a-1${e}^{\frac{1}{a}}$,即2a-1≥b2a-1恒成立,
由2a∈[3,m+1],令2a-1=t∈[2,m],则t≥bt,
所以lnb≤$\frac{lnt}{t}$=g(t),
由g′(t)=$\frac{1-lnt}{{t}^{2}}$,g(t)在(0,e)上递增,(e,+∞)上递减,且g(2)=g(4),
当2<m≤4时,g(t)min=g(2)=$\frac{ln2}{2}$,从而lnb≤$\frac{ln2}{2}$,解得:0<b≤$\sqrt{2}$;
当m>4时,g(t)min=g(m)=$\frac{lnm}{m}$,从而lnb≤$\frac{lnm}{m}$,解得:0<b≤${m}^{\frac{1}{m}}$,
故:当2<m≤4时,0<b≤$\sqrt{2}$;
当m>4时,0<b≤${m}^{\frac{1}{m}}$.
点评 本题主要考察利用导数求函数的单调区间,考察分类讨论思想及转化思想,考察学生分析问题解决问题得能力,属于中档题.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
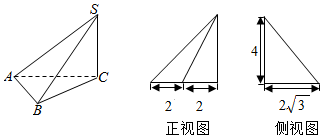 三棱锥S-ABC及其三视图的正视图和俯视图如图所示,则该三棱锥的外接球的表面积是( )
三棱锥S-ABC及其三视图的正视图和俯视图如图所示,则该三棱锥的外接球的表面积是( )| A. | $\frac{112}{3}$π | B. | $\frac{64}{3}$π | C. | 32π | D. | 64π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
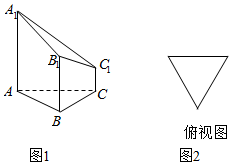 如图1是一个正三棱柱被平面A1B1C1截得的几何体,其中AB=2,AA1=3,BB1=2,CC1=1,几何体的俯视图如图2,则该几何体的正视图是( )
如图1是一个正三棱柱被平面A1B1C1截得的几何体,其中AB=2,AA1=3,BB1=2,CC1=1,几何体的俯视图如图2,则该几何体的正视图是( )| A. | 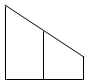 | B. | 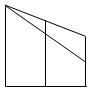 | C. | 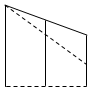 | D. | 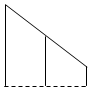 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}-1}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{6}-1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com