
分析 (1)由四边形A1B1A2B2面积4,得ab=2,由椭圆的离心率为$\frac{\sqrt{3}}{2}$,得$\frac{c}{a}=\frac{\sqrt{3}}{2}$,由此求出a,b,从而能求出椭圆C的方程.
(2)由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{y=kx+m}\end{array}\right.$,得(4k2+1)x2+8kmx+4m2-4=0,由此利用弦长公式、根的判别式、直线垂直、圆的性质,结合已知条件,能求出直线l被圆O截得的弦长.
解答 解:(1)∵四边形A1B1A2B2与四边形F1B1F2B2的面积为4.
∴$\frac{1}{2}$×2a×2b=4,∴ab=2,
∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,
∴$\frac{c}{a}=\frac{\sqrt{3}}{2}$,结合a2=b2+c2,得c=$\frac{\sqrt{3}}{2}$a,b=$\frac{1}{2}a$,(2分)
∴a2=4,则b=1,∴椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1.(5分)
(2)由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{y=kx+m}\end{array}\right.$,得(4k2+1)x2+8kmx+4m2-4=0,
设点M(x1,y1),N(x2,y2),则△=64k2m2-4(4k2+1)(4m2-4)>0,
即m2<4k2+1,${x}_{1}+{x}_{2}=-\frac{km}{4{k}^{2}+1}$,${x}_{1}{x}_{2}=\frac{4{m}^{2}-4}{4{k}^{2}+1}$,(8分)
则${y}_{1}{y}_{2}=(k{x}_{1}+m)(k{x}_{2}+m)={k}^{2}{x}_{1}{x}_{2}+km({x}_{1}+{x}_{2})+{m}^{2}$,
由OM⊥ON,得$\overrightarrow{OM}•\overrightarrow{ON}=0$,即x1x2+y1y2=0,
∴$({k}^{2}+1){x}_{1}{x}_{2}+km({x}_{1}+{x}_{2})+{m}^{2}$=0,即(k2+1)•$\frac{4{m}^{2}-4}{4{k}^{2}+1}$+km•(-$\frac{8km}{4{k}^{2}+1}$)+m2=0,
整理可得${m}^{2}=\frac{4{k}^{2}+4}{5}$,即|m|=$\frac{2\sqrt{5}•\sqrt{{k}^{2}+1}}{5}$,①
把①代入m2<4k2+1,得,该不等式恒成立.(10分)
以F1F2为直径的圆的圆心为(0,0),半径为$\sqrt{3}$.
圆心O到直线l的距离为d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$=$\frac{2\sqrt{5}}{5}$,
则直线l被圆O截得的弦长为:2$\sqrt{3-\frac{4}{5}}=\frac{2\sqrt{55}}{5}$.(12分)
点评 本题考查椭圆方程求法,考查弦长的求法,考查椭圆、韦达定理、根的判别式、直线方程、弦长公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $y=2sin(\frac{x}{3}-\frac{π}{6})$ | B. | $y=\frac{1}{2}sin(3x+\frac{π}{6})$ | C. | $y=\frac{1}{2}sin(3x-\frac{π}{6})$ | D. | $y=\frac{1}{2}sin(\frac{x}{3}-\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinα)>f(cosβ) | B. | f(cosα)<f(cosβ) | C. | f(sinα)<f(cosβ) | D. | f(sinα)<f(sinβ) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $[3,\frac{7}{2}]$ | B. | $[1,\frac{5}{4}]$ | C. | [63,71] | D. | [127,143] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\frac{2}{3}$ | B. | $\frac{4}{3}$或$\frac{2}{3}$ | C. | -1或1 | D. | $-\frac{4}{3}$或$-\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
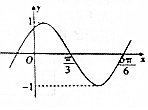 已知函数y=sin(ωx+φ)(ω>0,0<φ≤$\frac{π}{2}$)的部分图象如图所示,则cos(5ωφ)=-$\frac{1}{2}$.
已知函数y=sin(ωx+φ)(ω>0,0<φ≤$\frac{π}{2}$)的部分图象如图所示,则cos(5ωφ)=-$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com