练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知，若对于所有的恒成立，求实数的取值范围.

    实数的取值范围为或或.

    解析试题分析：对于所有的恒成立，即的最大值都小于
    等于；即对于所有的恒成立，
    令，只要，即可解出实数的取值范围．
    容易得出，
    即的最大值为1,
    则对于所有的恒成立
    对于所有的恒成立，
    即对于所有的恒成立，
    令，只要，∴或或．
    考点：恒成立问题、等价转换思想.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    在自然条件下，某草原上野兔第n年年初的数量记为xn,该年的增长量yn和 xn与的乘积成正比，比例系数为，其中m是与n无关的常数，且x1<m，
    (1)证明：;
    (2)用 xn表示xn+1;并证明草原上的野兔总数量恒小于m.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)＝ax2－2ax＋2＋b(a≠0)，若f(x)在区间[2,3]上有最大值5，最小值2.
    (1)求a，b的值；
    (2)若b<1，g(x)＝f(x)－mx在[2,4]上单调，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知.
    (1)当,时,若不等式恒成立,求的范围；
    (2)试判断函数在内零点的个数，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

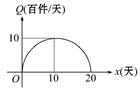
    某食品公司为了解某种新品种食品的市场需求,进行了20天的测试,人为地调控每天产品的单价P(元/件)：前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如表：

    时间(将第x天记为x)x
    		1
    		10
    		11
    		18
    单价(元/件)P
    		9
    		0
    		1
    		8
    而这20天相应的销售量Q(百件/天)与x对应的点(x,Q)在如图所示的半圆上.

    (1)写出每天销售收入y(元)与时间x(天)的函数关系式y=f(x).
    (2)在这20天中哪一天销售收入最高?为使每天销售收入最高,按此次测试结果应将单价P定为多少元为好?(结果精确到1元)

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知二次函数的二次项系数为，且不等式的解集为（1，3）．
    ⑴若方程有两个相等实数根，求的解析式．
    ⑵若的最大值为正数，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    为了保护环境，某工厂在国家的号召下，把废弃物回收转化为某种产品，经测算，处理成本（万元）与处理量（吨）之间的函数关系可近似的表示为：
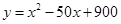    ，且每处理一吨废弃物可得价值为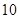万元的某种产品，同时获得国家补贴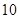万元．
    （1）当时，判断该项举措能否获利？如果能获利，求出最大利润；
    如果不能获利，请求出国家最少补贴多少万元，该工厂才不会亏损？
    （2）当处理量为多少吨时，每吨的平均处理成本最少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知lgx＋lgy＝2 lg(2x－3y)，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数y＝2－x2＋ax＋1在区间(－∞，3)内递增，求a的取值范围．

    查看答案和解析>>

    同步练习册答案