
在自然条件下,某草原上野兔第n年年初的数量记为xn,该年的增长量yn和 xn与 的乘积成正比,比例系数为
的乘积成正比,比例系数为 ,其中m是与n无关的常数,且x1<m,
,其中m是与n无关的常数,且x1<m,
(1)证明: ;
;
(2)用 xn表示xn+1;并证明草原上的野兔总数量恒小于m.
(1)详见解析;(2) ,证明用数学归纳法,过程详见解析.
,证明用数学归纳法,过程详见解析.
解析试题分析:(1)由已知可得yn是xn的一个二次函数,利用配方法,注意到 就可证明
就可证明 ;(2)由已知有该年的增长量
;(2)由已知有该年的增长量 ,所以第n+1年年初的的数量xn+1=xn+yn,代入即可用 xn表示xn+1;证明草原上的野兔总数量恒小于m,即证对一切非零自然数n,都有xn<m,可考虑用数学归纳法来证明:当n=1时显然成立;再假设当
,所以第n+1年年初的的数量xn+1=xn+yn,代入即可用 xn表示xn+1;证明草原上的野兔总数量恒小于m,即证对一切非零自然数n,都有xn<m,可考虑用数学归纳法来证明:当n=1时显然成立;再假设当 时,命题成立,则对n=k+1时,由于
时,命题成立,则对n=k+1时,由于 是xk的一个二次函数,结合二次函数的性质,可证
是xk的一个二次函数,结合二次函数的性质,可证 成立,从而有对一切正整数n,
成立,从而有对一切正整数n,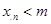 ,即是草原上的野兔总数量恒小于m.
,即是草原上的野兔总数量恒小于m.
试题解析:(1)由题意知 ,配方得:
,配方得: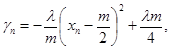 ∵
∵ ∴当且仅当
∴当且仅当 时,
时, 取得最大值
取得最大值 ,即
,即 (5分)
(5分)
(2) (8分)
(8分)
用数列归纳法证明:
当n=1时,由题意知 ,故命题成立
,故命题成立
假设当 时,命题成立
时,命题成立 是xk的一个二次函数
是xk的一个二次函数 ,
, 有对称轴
有对称轴 ,开口向下,由
,开口向下,由 ,则
,则 ,于是在
,于是在 上均有
上均有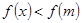 =m
=m
取 ,即知
,即知 ,∴当
,∴当 时,命题成立,综上知,对一切正整数n,
时,命题成立,综上知,对一切正整数n,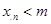 这就是说该草原上的野兔数量不可能无限增长 (13分)
这就是说该草原上的野兔数量不可能无限增长 (13分)
考点:1函数的概念;2.二次函数;3.数学归纳法.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
已知二次函数f(x)=ax2+bx+c(a>0).
(Ⅰ)(i)若b=﹣2,且f(x)在(1,+∞)上为单调递增函数,求实数a的取值范围;
(ii)若b=﹣1,c=1,当x∈[0,1]时,|f(x)|的最大值为1,求实数a的取值范围;
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,求a的最小正整数值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,函数
,函数 .
.
⑴当 时,函数
时,函数 的图象与函数
的图象与函数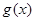 的图象有公共点,求实数
的图象有公共点,求实数 的最大值;
的最大值;
⑵当 时,试判断函数
时,试判断函数 的图象与函数
的图象与函数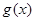 的图象的公共点的个数;
的图象的公共点的个数;
⑶函数 的图象能否恒在函数
的图象能否恒在函数 的上方?若能,求出
的上方?若能,求出 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某厂生产A产品的年固定成本为250万元,若A产品的年产量为 万件,则需另投入成本
万件,则需另投入成本 (万元)。已知A产品年产量不超过80万件时,
(万元)。已知A产品年产量不超过80万件时, ;A产品年产量大于80万件时,
;A产品年产量大于80万件时, 。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。
。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。
(1)写出L关于 的函数解析式
的函数解析式 ;
;
(2)当年产量为多少时,该厂生产A产品所获的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某小区想利用一矩形空地 建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中
建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中 ,
, ,且
,且 中,
中, ,经测量得到
,经测量得到 .为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点
.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点 作一直线交
作一直线交 于
于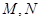 ,从而得到五边形
,从而得到五边形 的市民健身广场,设
的市民健身广场,设 .
.
(1)将五边形 的面积
的面积 表示为
表示为 的函数;
的函数;
(2)当 为何值时,市民健身广场的面积最大?并求出最大面积.
为何值时,市民健身广场的面积最大?并求出最大面积.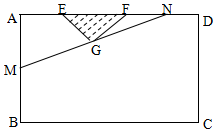
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com