
已知函数f(x)=x2+ax+1,f(x)在x∈[-3,1 上恒有f(x)
上恒有f(x)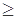 -3成立,求实数a 的取值范围.
-3成立,求实数a 的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
某市粮食储备库的设计容量为30万吨,年初库存粮食10万吨,从1月份起,计划每月收购粮食M万吨,每月供给市面粉厂粮食1万吨,另外每月还有大量的粮食外调任务。已知n个月内外调粮食的总量为 万吨与n的函数关系为
万吨与n的函数关系为 .要使在16个月内每月粮食收购之后能满足内、外调需要,且每月粮食调出后粮库内有不超过设计容量的储备粮,求M的范围。
.要使在16个月内每月粮食收购之后能满足内、外调需要,且每月粮食调出后粮库内有不超过设计容量的储备粮,求M的范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在自然条件下,某草原上野兔第n年年初的数量记为xn,该年的增长量yn和 xn与 的乘积成正比,比例系数为
的乘积成正比,比例系数为 ,其中m是与n无关的常数,且x1<m,
,其中m是与n无关的常数,且x1<m,
(1)证明: ;
;
(2)用 xn表示xn+1;并证明草原上的野兔总数量恒小于m.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某厂生产某种产品的年固定成本为250万元,每生产 万件,需另投入的成本为
万件,需另投入的成本为 (单位:万元),当年产量小于80万件时,
(单位:万元),当年产量小于80万件时, ;当年产量不小于80万件时,
;当年产量不小于80万件时, .假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完.
.假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (万件)的函数关系式;
(万件)的函数关系式;
(2)年产量为多少万件时,该厂在该产品的生产中所获利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
若整数
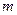 满足不等式
满足不等式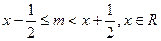 ,则称
,则称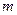 为
为 的“亲密整数”,记作
的“亲密整数”,记作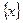 ,即
,即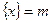 ,已知函数
,已知函数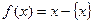 .给出以下四个命题:
.给出以下四个命题:
① 函数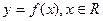 是周期函数且其最小正周期为
是周期函数且其最小正周期为 1;
1;
② 函数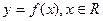 的图象关于点
的图象关于点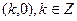 中心对称;
中心对称;
③ 函数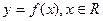 在
在 上单调递增;
上单调递增;
④ 方程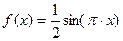 在
在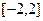 上共有7个不相等的实数根.
上共有7个不相等的实数根.
其中正确命题的序号是 .(写出所有正确命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com