
已知 .
.
(1)当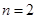 ,
, 时,若不等式
时,若不等式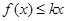 恒成立,求
恒成立,求 的范围;
的范围;
(2)试判断函数 在
在 内零点的个数,并说明理由.
内零点的个数,并说明理由.
科目:高中数学 来源: 题型:解答题
某书商为提高某套丛书的销量,准备举办一场展销会.据市场调查,当每套丛书售价定为x元时,销售量可达到15—0.1x万套.现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10.假设不计其他成本,即销售每套丛书的利润=售价-供货价格.问:
(1)每套丛书售价定为100元时,书商能获得的总利润是多少万元?
(2)每套丛书售价定为多少元时,单套丛书的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数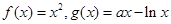 ,
,
(1)若函数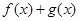 在
在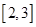 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(2)是否存在实数 ,当
,当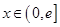 (
(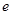 是自然常数)时,函数
是自然常数)时,函数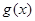 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)当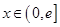 时,证明:
时,证明: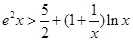 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com