
已知函数 .
.
(1)求 的解集;
的解集;
(2)设函数
 ,若
,若 对任意的
对任意的 都成立,求
都成立,求 的取值范围.
的取值范围.
(1)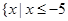 或
或 ;(2)
;(2) .
.
解析试题分析:本题主要考查绝对值不等式的解法、分段函数图象、直线图象等基础知识,考查学生的转化能力、计算能力和数形结合思想.第一问,先将被开方数写成完全平方式,开方需要加绝对值,解绝对值不等式,利用零点分段法去掉绝对值符号,解不等式组;第二问,“ 对任意的
对任意的 都成立”转化为“
都成立”转化为“ 的图象恒在
的图象恒在 图象的上方”利用零点分段法将绝对值去掉,转化成分段函数,画出分段函数图象,而
图象的上方”利用零点分段法将绝对值去掉,转化成分段函数,画出分段函数图象,而 恒过(3,0)点,将
恒过(3,0)点,将 的直线绕(3,0)点旋转,找出符合题意的位置,得到k的取值范围.
的直线绕(3,0)点旋转,找出符合题意的位置,得到k的取值范围.
试题解析:(1)

∴ 即
即

∴ ① 或
① 或 ② 或
② 或 ③
③
解得不等式①: ;②:无解 ③:
;②:无解 ③:
所以 的解集为
的解集为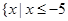 或
或 . 5分
. 5分
(2) 即
即 的图象恒在
的图象恒在 图象的上方
图象的上方
 图象为恒过定点
图象为恒过定点
 ,且斜率
,且斜率 变化的一条直线作函数
变化的一条直线作函数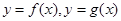 图象如图,
图象如图,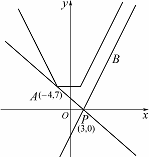
其中 ,
, ,∴
,∴
由图可知,要使得 的图象恒在
的图象恒在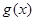 图象的上方
图象的上方
∴实数 的取值范围为
的取值范围为 . 10分
. 10分
考点:绝对值不等式的解法、分段函数图象、直线图象.


科目:高中数学 来源: 题型:解答题
某厂生产某种产品的年固定成本为250万元,每生产 万件,需另投入的成本为
万件,需另投入的成本为 (单位:万元),当年产量小于80万件时,
(单位:万元),当年产量小于80万件时, ;当年产量不小于80万件时,
;当年产量不小于80万件时, .假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完.
.假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (万件)的函数关系式;
(万件)的函数关系式;
(2)年产量为多少万件时,该厂在该产品的生产中所获利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=xk+b(其中k,b∈R且k,b为常数)的图象经过A(4,2)、B(16,4)两点.
(1)求f(x)的解析式;
(2)如果函数g(x)与f(x)的图象关于直线y=x对称,解关于x的不等式:g(x)+g(x-2)>2a(x-2)+4.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
据市场分析,广饶县驰中集团某蔬菜加工点,当月产量在10吨至25吨时,月生产总成本 (万元)可以看成月产量
(万元)可以看成月产量 (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(1)写出月总成本 (万元)关于月产量
(万元)关于月产量 (吨)的函数关系;
(吨)的函数关系;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润;
(3)当月产量为多少吨时, 每吨平均成本最低,最低成本是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数f(x)= -ax2,a∈R.
-ax2,a∈R.
(1)当a=2时,求函数f(x)的零点;
(2)当a>0时,求证:函数f(x)在(0,+∞)内有且仅有一个零点;
(3)若函数f(x)有四个不同的零点,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com