
已知函数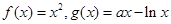 ,
,
(1)若函数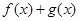 在
在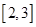 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(2)是否存在实数 ,当
,当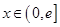 (
(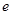 是自然常数)时,函数
是自然常数)时,函数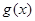 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)当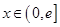 时,证明:
时,证明: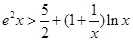 .
.
(1) ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
解析试题分析:(1)先对函数 进行求导,根据函数h(x)在[2,3]上是减函数,可得到其导函数在[2,3]上小于等于0应该恒成立,再结合二次函数的性质可求得a的范围;(2)先假设存在,然后对函数g(x)进行求导,再对a的值分情况讨论函数g(x)在(0,e]上的单调性和最小值取得,可知当a=e2能够保证当x∈(0,e]时g(x)有最小值3;(3)结合(2)知
进行求导,根据函数h(x)在[2,3]上是减函数,可得到其导函数在[2,3]上小于等于0应该恒成立,再结合二次函数的性质可求得a的范围;(2)先假设存在,然后对函数g(x)进行求导,再对a的值分情况讨论函数g(x)在(0,e]上的单调性和最小值取得,可知当a=e2能够保证当x∈(0,e]时g(x)有最小值3;(3)结合(2)知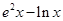 的最小值为3,只须证明
的最小值为3,只须证明 即可,令
即可,令 ,则
,则 在
在 上单调递增,∴
上单调递增,∴ 的最大值为
的最大值为
 故
故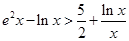 ,即
,即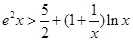 得证.
得证.
解:(1)令 ,则
,则 ,
, (1分))∵
(1分))∵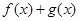 在
在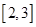 上是减函数,
上是减函数,
∴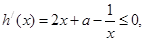 在
在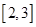 上恒成立,即
上恒成立,即 在
在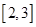 上恒成立 (2分)
上恒成立 (2分)
而 在
在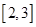 上是减函数,∴
上是减函数,∴ 的最小值为
的最小值为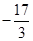
 (4分)
(4分)
(2)假设存在实数 ,使
,使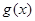 有最小值是3,∵
有最小值是3,∵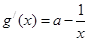 ,
,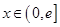
若 ,则
,则 ,∴
,∴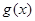 在
在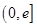 上为减函数,
上为减函数,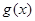 的最小值为
的最小值为
∴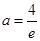 与
与 矛盾, (5分)
矛盾, (5分)
若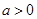 时,令
时,令 ,则
,则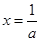
当 ,即
,即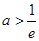 ,
,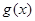 在
在 上单调递减,在
上单调递减,在 上单调递增
上单调递增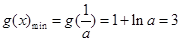 ,解得
,解得 (7分)
(7分)
当 ,即
,即 时,
时,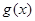 在
在 上单调递减
上单调递减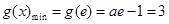
∴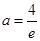 与
与 矛盾, (9分)
矛盾, (9分)
(3)∵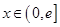 ,由
,由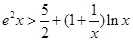 整理得
整理得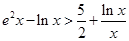 , (10分)
, (10分)
而由(2)知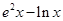 的最小值为3,只须证明
的最小值为3,只须证明 即可 (11分))
即可 (11分))
令 ,则
,则 在
在 上单调递增,
上单调递增,
∴ 的最大值为
的最大值为
 (12分)
(12分)
故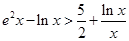 ,即
,即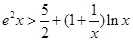 (14分)
(14分)
(接11分处另解, 即证 ,即证
,即证

科目:高中数学 来源: 题型:解答题
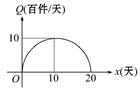
某食品公司为了解某种新品种食品的市场需求,进行了20天的测试,人为地调控每天产品的单价P(元/件):前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如表:
| 时间(将第x天记为x)x | 1 | 10 | 11 | 18 |
| 单价(元/件)P | 9 | 0 | 1 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=xk+b(其中k,b∈R且k,b为常数)的图象经过A(4,2)、B(16,4)两点.
(1)求f(x)的解析式;
(2)如果函数g(x)与f(x)的图象关于直线y=x对称,解关于x的不等式:g(x)+g(x-2)>2a(x-2)+4.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)= 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.
(1)求实数a的值组成的集合A;
(2)设x1、x2是关于x的方程f(x)= 的两个相异实根,若对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围.
的两个相异实根,若对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com