
已知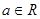 ,函数
,函数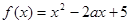 .
.
⑴若不等式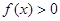 对任意
对任意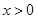 恒成立,求实数
恒成立,求实数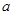 的最值范围;
的最值范围;
⑵若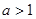 ,且函数
,且函数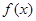 的定义域和值域均为
的定义域和值域均为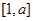 ,求实数
,求实数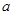 的值.
的值.
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:填空题
设函数f(x)的定义域为R,若存在常数M>0,使得|f(x)|≤M|x|对一切实数x均成立,则称f(x)为F函数,给出下列函数:
①f(x)=0; ②f(x)=x2; ③f(x)= (sinx+cosx); ④f(x)=
(sinx+cosx); ④f(x)= ;
;
⑤f(x)是定义在R上的奇函数,且对于任意实数x1,x2,均有|f(x1)-f(x2)|≤2|x1-x2|。
则其中是F函数的序号是___________________
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某厂生产A产品的年固定成本为250万元,若A产品的年产量为 万件,则需另投入成本
万件,则需另投入成本 (万元)。已知A产品年产量不超过80万件时,
(万元)。已知A产品年产量不超过80万件时, ;A产品年产量大于80万件时,
;A产品年产量大于80万件时, 。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。
。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。
(1)写出L关于 的函数解析式
的函数解析式 ;
;
(2)当年产量为多少时,该厂生产A产品所获的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某小区想利用一矩形空地 建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中
建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中 ,
, ,且
,且 中,
中, ,经测量得到
,经测量得到 .为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点
.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点 作一直线交
作一直线交 于
于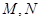 ,从而得到五边形
,从而得到五边形 的市民健身广场,设
的市民健身广场,设 .
.
(1)将五边形 的面积
的面积 表示为
表示为 的函数;
的函数;
(2)当 为何值时,市民健身广场的面积最大?并求出最大面积.
为何值时,市民健身广场的面积最大?并求出最大面积.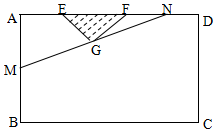
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某书商为提高某套丛书的销量,准备举办一场展销会.据市场调查,当每套丛书售价定为x元时,销售量可达到15—0.1x万套.现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10.假设不计其他成本,即销售每套丛书的利润=售价-供货价格.问:
(1)每套丛书售价定为100元时,书商能获得的总利润是多少万元?
(2)每套丛书售价定为多少元时,单套丛书的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数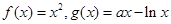 ,
,
(1)若函数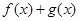 在
在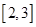 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(2)是否存在实数 ,当
,当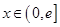 (
(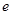 是自然常数)时,函数
是自然常数)时,函数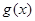 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)当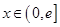 时,证明:
时,证明: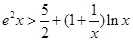 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com