
某厂生产A产品的年固定成本为250万元,若A产品的年产量为 万件,则需另投入成本
万件,则需另投入成本 (万元)。已知A产品年产量不超过80万件时,
(万元)。已知A产品年产量不超过80万件时, ;A产品年产量大于80万件时,
;A产品年产量大于80万件时, 。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。
。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。
(1)写出L关于 的函数解析式
的函数解析式 ;
;
(2)当年产量为多少时,该厂生产A产品所获的利润最大?
科目:高中数学 来源: 题型:解答题
在自然条件下,某草原上野兔第n年年初的数量记为xn,该年的增长量yn和 xn与 的乘积成正比,比例系数为
的乘积成正比,比例系数为 ,其中m是与n无关的常数,且x1<m,
,其中m是与n无关的常数,且x1<m,
(1)证明: ;
;
(2)用 xn表示xn+1;并证明草原上的野兔总数量恒小于m.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
用总长为14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某房地产开发商投资81万元建一座写字楼,第一年需维护费用为1万元,以后每年增加2万元,若把写字楼出租,每年收入租金30万元.
(1)开发商最早在第几年获取纯利润?
(2)若干年后开发商为了投资其它项目,有两种处理方案:①纯利润最大时,以10万元出售该楼;②年平均利润最大时以46万元出售该楼.问哪种方案更优?并说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
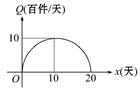
某食品公司为了解某种新品种食品的市场需求,进行了20天的测试,人为地调控每天产品的单价P(元/件):前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如表:
| 时间(将第x天记为x)x | 1 | 10 | 11 | 18 |
| 单价(元/件)P | 9 | 0 | 1 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com