某市粮食储备库的设计容量为30万吨，年初库存粮食10万吨，从1月份起，计划每月收购粮食M万吨，每月供给市面粉厂粮食1万吨，另外每月还有大量的粮食外调任务。已知n个月内外调粮食的总量为
万吨与n的函数关系为
．要使在16个月内每月粮食收购之后能满足内、外调需要，且每月粮食调出后粮库内有不超过设计容量的储备粮，求M的范围。
口算能手系列答案科目：高中数学 来源： 题型：填空题
设函数f(x)的定义域为R，若存在常数M>0，使得|f(x)|≤M|x|对一切实数x均成立，则称f(x)为F函数，给出下列函数：
①f(x)=0； ②f(x)=x2； ③f(x)=
(sinx+cosx)； ④f(x)=
；
⑤f(x)是定义在R上的奇函数，且对于任意实数x1，x2，均有|f(x1)－f(x2)|≤2|x1－x2|。
则其中是F函数的序号是___________________
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知二次函数f（x）=ax2+bx+c（a＞0）．
（Ⅰ）（i）若b=﹣2，且f（x）在（1，+∞）上为单调递增函数，求实数a的取值范围；
（ii）若b=﹣1，c=1，当x∈[0，1]时，|f（x）|的最大值为1，求实数a的取值范围；
（Ⅱ）若f（0）≥1，f（1）≥1，f（x）=0的有两个小于1的不等正根，求a的最小正整数值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
=
（
，
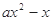（1）当
时，判断函数
在定义域上的单调性；
（2）若函数
与
的图像有两个不同的交点
，求
的取值范围。
（3）设点
和
（
是函数图像上的两点，平行于
的切线以
为切点，求证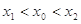
.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某书商为提高某套丛书的销量，准备举办一场展销会．据市场调查，当每套丛书售价定为x元时，销售量可达到15—0.1x万套．现出版社为配合该书商的活动，决定进行价格改革，将每套丛书的供货价格分成固定价格和浮动价格两部分，其中固定价格为30元，浮动价格(单位：元)与销售量(单位：万套)成反比，比例系数为10.假设不计其他成本，即销售每套丛书的利润＝售价－供货价格．问：
(1)每套丛书售价定为100元时，书商能获得的总利润是多少万元？
(2)每套丛书售价定为多少元时，单套丛书的利润最大？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
万吨，则
， 可以看成是
的二次函数式，根据题设，利用
找出不等关系，求解.
，则
，
可知：M的范围为
），试求出此函数的解析式，并写出其定义域，判断奇偶性，单调性．
上恒有f(x)
－3成立，求实数a 的取值范围.
必过定点 
则
的解集为________.