
已知二次函数f(x)=ax2+bx+c(a>0).
(Ⅰ)(i)若b=﹣2,且f(x)在(1,+∞)上为单调递增函数,求实数a的取值范围;
(ii)若b=﹣1,c=1,当x∈[0,1]时,|f(x)|的最大值为1,求实数a的取值范围;
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,求a的最小正整数值.
(Ⅰ)(i)[1,+∞);(ii)(0,1];(Ⅱ)5
解析试题分析:(Ⅰ)(i)若b=﹣2,则f(x)=ax2﹣2x+c(a>0)的图象是开口朝上且以直线x= 为对称轴的抛物线.若f(x)在(1,+∞)上为单调递增函数,则
为对称轴的抛物线.若f(x)在(1,+∞)上为单调递增函数,则 ≤1,解得a≥1,即实数a的取值范围为[1,+∞);(ii)若b=﹣1,c=1,则f(x)=ax2﹣x+1(a>0)的图象是开口朝上且以直线x=
≤1,解得a≥1,即实数a的取值范围为[1,+∞);(ii)若b=﹣1,c=1,则f(x)=ax2﹣x+1(a>0)的图象是开口朝上且以直线x= 为对称轴的抛物线,若当x∈[0,1]时,|f(x)|的最大值为1,则
为对称轴的抛物线,若当x∈[0,1]时,|f(x)|的最大值为1,则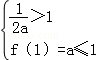 或
或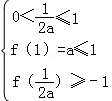 解得0<a<
解得0<a<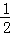 ,或
,或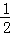 ≤a≤1,所以实数a的取值范围为(0,1];(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,则
≤a≤1,所以实数a的取值范围为(0,1];(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,则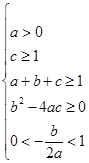
解得a>4,故a的最小正整数值为5.
试题解析:(Ⅰ)(i)若b=﹣2,
则f(x)=ax2﹣2x+c(a>0)的图象是开口朝上且以直线x= 为对称轴的抛物线.
为对称轴的抛物线.
若f(x)在(1,+∞)上为单调递增函数,则 ≤1,解得a≥1,
≤1,解得a≥1,
即实数a的取值范围为[1,+∞)
(ii)若b=﹣1,c=1,
则f(x)=ax2﹣x+1(a>0)的图象是开口朝上且以直线x= 为对称轴的抛物线.
为对称轴的抛物线.
若当x∈[0,1]时,|f(x)|的最大值为1,
则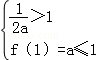 或
或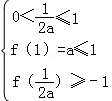 ,
,
解得0<a<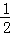 ,或
,或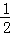 ≤a≤1
≤a≤1
综上所述:0<a≤1
即实数a的取值范围为(0,1]
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,
则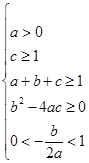
由b2>4ac>4a(1﹣a﹣b)得:
b2+4ab+4a2=(b+2a)2>4a,
即b+2a>2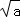 ,
,
即b>2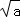 ﹣2a,…①
﹣2a,…①
由b2>4ac≥4a得:
b<﹣2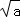 …②
…②
由①②得:
2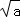 ﹣2a<﹣2
﹣2a<﹣2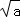 ,
,
解得a>4,
故a的最小正整数值为5.
考点:1.二次函数的图象与性质;2.不等式的性质


科目:高中数学 来源: 题型:解答题
某市粮食储备库的设计容量为30万吨,年初库存粮食10万吨,从1月份起,计划每月收购粮食M万吨,每月供给市面粉厂粮食1万吨,另外每月还有大量的粮食外调任务。已知n个月内外调粮食的总量为 万吨与n的函数关系为
万吨与n的函数关系为 .要使在16个月内每月粮食收购之后能满足内、外调需要,且每月粮食调出后粮库内有不超过设计容量的储备粮,求M的范围。
.要使在16个月内每月粮食收购之后能满足内、外调需要,且每月粮食调出后粮库内有不超过设计容量的储备粮,求M的范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在自然条件下,某草原上野兔第n年年初的数量记为xn,该年的增长量yn和 xn与 的乘积成正比,比例系数为
的乘积成正比,比例系数为 ,其中m是与n无关的常数,且x1<m,
,其中m是与n无关的常数,且x1<m,
(1)证明: ;
;
(2)用 xn表示xn+1;并证明草原上的野兔总数量恒小于m.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
记不超过x的最大整数为 ,令
,令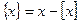 ,则函数
,则函数 : ①定义域为R; ②值域为
: ①定义域为R; ②值域为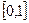 ;③在定义域上是单调增函数; ④是周
;③在定义域上是单调增函数; ④是周 期为1的周期函数; ⑤是奇函数。其中正确判断的序号是_________________(把所有正确的序号都填上)
期为1的周期函数; ⑤是奇函数。其中正确判断的序号是_________________(把所有正确的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com