
已知函数 ,函数
,函数 .
.
⑴当 时,函数
时,函数 的图象与函数
的图象与函数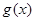 的图象有公共点,求实数
的图象有公共点,求实数 的最大值;
的最大值;
⑵当 时,试判断函数
时,试判断函数 的图象与函数
的图象与函数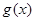 的图象的公共点的个数;
的图象的公共点的个数;
⑶函数 的图象能否恒在函数
的图象能否恒在函数 的上方?若能,求出
的上方?若能,求出 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.
(1) 的最大值为
的最大值为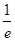 ,(2)
,(2)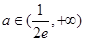 时,无公共点,
时,无公共点,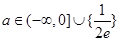 时,有一个公共点,
时,有一个公共点,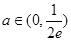 时,有两个公共点;(3)当
时,有两个公共点;(3)当 或
或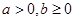 时函数
时函数 的图象恒在函数
的图象恒在函数 的图象的上方.
的图象的上方.
解析试题分析:(1)当 时,由图形可知一次函数
时,由图形可知一次函数 与对数函数
与对数函数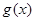 相切时,
相切时, 取最大值,可以用导数的几何意义完成;(2)要研究两函数的公共点个数,由函数
取最大值,可以用导数的几何意义完成;(2)要研究两函数的公共点个数,由函数 的定义域可知只需考虑
的定义域可知只需考虑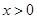 情况,当
情况,当 时,令
时,令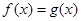 得
得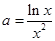 ,则原命题等价于研究直线
,则原命题等价于研究直线 与函数
与函数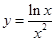 的图象的公共点的个数,因此利用导数研究函数
的图象的公共点的个数,因此利用导数研究函数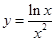 图象变化情况,易得结论;(3)把问题转化为:
图象变化情况,易得结论;(3)把问题转化为: 在
在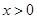 时恒成立问题,要注意对
时恒成立问题,要注意对 取值情况的讨论.
取值情况的讨论.
试题解析:⑴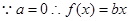 ,由一次函数与对数函数图象可知两图象相切时
,由一次函数与对数函数图象可知两图象相切时 取最大值,设切点横坐标为
取最大值,设切点横坐标为 ,
,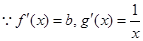 ,
,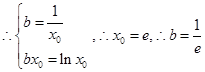 , 即实数
, 即实数 的最大值为
的最大值为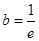 ,⑵
,⑵ ,即原题等价于直线
,即原题等价于直线 与函数
与函数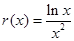 的图象的公共点的个数,
的图象的公共点的个数,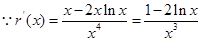 ,
,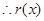 在
在 递增且
递增且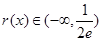 ,
,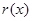 在
在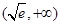 递减且
递减且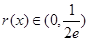 ,
,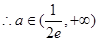 时,无公共点,
时,无公共点,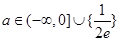 时,有一个公共点,
时,有一个公共点,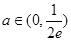 时,有两个公共点;⑶函数
时,有两个公共点;⑶函数 的图象恒在函数
的图象恒在函数 的上方;即
的上方;即 在
在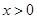 时恒成立,①
时恒成立,①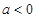 时
时 图象开口向下,即
图象开口向下,即 在
在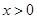 时不可能恒成立,②
时不可能恒成立,②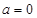 时
时 ,由⑴可得
,由⑴可得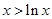 ,
, 时
时 恒成立,
恒成立,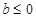 时
时 不成立,③
不成立,③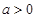 时,若
时,若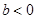 则
则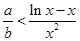 ,由⑵可得
,由⑵可得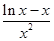 无最小值,故
无最小值,故 不可能恒成立,若
不可能恒成立,若 则
则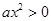 ,故
,故 恒成立,若
恒成立,若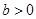 则
则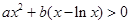 ,故
,故 恒成立,综上,
恒成立,综上, 或
或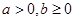 时,函数
时,函数 的图象恒在函数
的图象恒在函数 的图象的上方.
的图象的上方.
考点:导数的几何意义,用导数分析函数的单调性,最值,恒成立问题,渗透数形结合思想,分类讨论的数学思想


科目:高中数学 来源: 题型:解答题
在自然条件下,某草原上野兔第n年年初的数量记为xn,该年的增长量yn和 xn与 的乘积成正比,比例系数为
的乘积成正比,比例系数为 ,其中m是与n无关的常数,且x1<m,
,其中m是与n无关的常数,且x1<m,
(1)证明: ;
;
(2)用 xn表示xn+1;并证明草原上的野兔总数量恒小于m.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
用总长为14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某房地产开发商投资81万元建一座写字楼,第一年需维护费用为1万元,以后每年增加2万元,若把写字楼出租,每年收入租金30万元.
(1)开发商最早在第几年获取纯利润?
(2)若干年后开发商为了投资其它项目,有两种处理方案:①纯利润最大时,以10万元出售该楼;②年平均利润最大时以46万元出售该楼.问哪种方案更优?并说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=ax2-2ax+2+b(a≠0),若f(x)在区间[2,3]上有最大值5,最小值2.
(1)求a,b的值;
(2)若b<1,g(x)=f(x)-mx在[2,4]上单调,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com