已知函数f(x)=xex+ax2+2x+1在x=-1处取得极值.
(1)求函数f(x)的单调区间.
(2)若函数y=xex与y=-x2-2x+m的图象有惟一的交点,试求实数m的值.
解:(1)f
/(x)=e
x+xe
x+2ax+2=e
x(x+1)+2ax+2,
由f
/(-1)=0得-2a+2=0,
∴a=1,f(x)=xe
x+x
2+2x+1,
f
/(x)=e
x(x+1)+2x+2=(x+1)(e
x+2),
由f
/(x)>0,得x>-1;由f
/(x)<0,得x<-1;
故函数f(x)的单调增区间为(-1,+∞),单调减区间为(-∞,-1)
(2)函数y=xe
x与y=-x
2-2x+m的图象有惟一的交点等价于
方程xe
x=-x
2-2x+m,即f(x)=m+1有惟一解,
由(1)f(x)在(-∞,-1)递减,(-1,+∞)递增,
故f(x)在x=-1时取极小值(最小值)
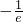
.
从而方程f(x)=m+1有惟一解的充要条件是
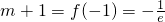
.
所以,函数y=xe
x与y=-x
2-2x+m的图象有惟一交点时
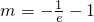
分析:(1)求出导函数,令导函数在x=-1处的值为0,列出方程,求出a,将a的值代入f(x),f′(x);令f′(x)>0求出递增区间,令f′(x)<0求出递减区间.
(2)将图象有惟一的交点转化为方程有唯一的解;将方程变形转化为f(x)与直线y=m+1有唯一解,由(1)求出f(x)的极小值,令极小值等于m+1求出m的值.
点评:本题考查函数在极值点处的导数值是0、考查利用导函数的符号判断函数的单调性、考查利用导数求函数的最值、考查等价转化的数学思想方法.

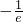 .
.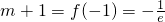 .
.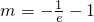


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<