
分析 (Ⅰ)求函数的定义域和导数,讨论a的取值,利用函数单调性和导数之间的关系即可讨论f(x)的单调性;
(Ⅱ)将不等式恒成立进行转化,根据条件构造函数研究函数的最值进行求解即可.
解答 解:(Ⅰ)函数的定义域为(0,+∞),
由题${f^'}(x)=\frac{a}{x}-\frac{{2{a^2}}}{x^2}+1=\frac{(x+2a)(x-a)}{x^2}(x>0)$…(2分)
(1)当a=0时,f′(x)=1>0,所以f(x)在(0,+∞)上递增
(2)当a>0时,由f′(x)<0得0<x<a,f′(x)>0得x>a
所以f(x)在(0,a)上递减,在(a,+∞)上递增
(3)当a<0时,由f′(x)<0得0<x<-2a,f′(x)>0得x>-2a
所以f(x)在(0,-2a)上递减,在(-2a,+∞)上递增
综上,a=0时,f(x)在(0,+∞)上递增,
a>0时,f(x)在(0,a)上递减,在(a,+∞)上递增,
a<0时,f(x)在(0,-2a)上递减,在(-2a,+∞)上递增…(6分)
(Ⅱ)若m>n,由$\frac{f(m)-f(n)}{m-n}<1$得f(m)-m<f(n)-n
若m<n,由$\frac{f(m)-f(n)}{m-n}<1$得f(m)-m>f(n)-n
令$g(x)=f(x)-x=alnx+\frac{{2{a^2}}}{x}$,所以g(x)在(0,e)上单调递减…(8分)
又${g^'}(x)=\frac{a}{x}-\frac{{2{a^2}}}{x^2}=\frac{a(x-2a)}{x^2}(x>0)$
(1)当a=0时,g(x)=0,不符合题意;
(2)当a>0时,由g′(x)<0得0<x<2a,g′(x)>0得x>2a
所以g(x)在(0,2a)上递减,在(2a,+∞)上递增
所以2a≥e,即$a≥\frac{e}{2}$
(3)当a<0时,在(0,+∞)上,都有g′(x)<0
所以g(x)在(0,+∞)上递减,即在(0,e)上也单调递减…(11分)
综上,实数a的取值范围为$(-∞,0)∪[\frac{e}{2},+∞)$…(12分)
点评 本题主要考查函数单调性和导数的关系以及不等式恒成立,注意对参数进行分类讨论,考查学生的运算和推理能力.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:解答题
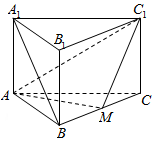 如图,已知三棱柱A1B1C1-ABC中,侧棱与底面垂直,AB=BC=AA1,∠ABC=90°,M是BC的中点.
如图,已知三棱柱A1B1C1-ABC中,侧棱与底面垂直,AB=BC=AA1,∠ABC=90°,M是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,AE=1.
边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,AE=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
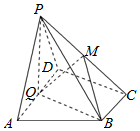 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢运动 | 不喜欢运动 | 总计 | |
| 男 | a= | b= | |
| 女 | c= | d= | |
| 总计 | n= |
| P(χ2≥x0) | 0.050 | 0.025 | 0.010 | 0.001 |
| x0 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{20}{3}π$ | B. | $\frac{25}{3}π$ | C. | $\frac{28}{3}π$ | D. | $\frac{32}{3}π$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com