
已知抛物线C顶点为原点,其焦点F(0,c)(c>0)到直线l:x-y-2=0的距离为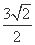 ,设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.
,设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.
(1)求抛物线C的方程;
(2)当点P(x0,y0)为直线l上的定点时,求直线AB的方程;
(3)当点P在直线l上移动时,求|AF|·|BF|的最小值.
解:(1)∵抛物线C的焦点F(0,c)(c>0)到直线l:x-y-2=0的距离为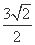 ,
,
∴ =
=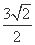 ,得c=1,
,得c=1,
∴F(0,1),即抛物线C的方程为x2=4y.
(2)设切点A(x1,y1),B(x2,y2),
由x2=4y得y′=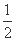 x,
x,
∴切线PA:y-y1=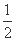 x1(x-x1),
x1(x-x1),
有y=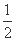 x1x-
x1x- +y1,而
+y1,而 =4y1,
=4y1,
即切线PA:y=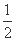 x1x-y1,
x1x-y1,
同理可得切线PB:y=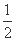 x2x-y2.
x2x-y2.
∵两切线均过定点P(x0,y0),
∴y0=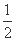 x1x0-y1,y0=
x1x0-y1,y0=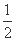 x2x0-y2,
x2x0-y2,
由此两式知点A,B均在直线y0=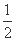 xx0-y上,
xx0-y上,
∴直线AB的方程为y0=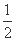 xx0-y,
xx0-y,
即y=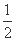 x0x-y0.
x0x-y0.
(3)设点P的坐标为(x′,y′),
由x′-y′-2=0,
得x′=y′+2,
则|AF|·|BF|= ·
·
= ·
·
= ·
·
=(y1+1)·(y2+1)
=y1y2+(y1+y2)+1.
由
得y2+(2y′-x′2)y+y′2=0,
有y1+y2=x′2-2y′,y1y2=y′2,
∴|AF|·|BF|=y′2+x′2-2y′+1
=y′2+(y′+2)2-2y′+1
=2 2+
2+ ,
,
当y′=-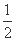 ,x′=
,x′=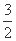 时,
时,
即P 时,|AF|·|BF|取得最小值
时,|AF|·|BF|取得最小值 .
.


科目:高中数学 来源: 题型:
已知抛物线y2=2px(p>0),过其焦点且斜率为1的直线交抛物线于A、B两点,若线段AB的中点的纵坐标为2,则该抛物线的准线方程为( )
(A)x=1 (B)x=-1
(C)x=2 (D)x=-2
查看答案和解析>>
科目:高中数学 来源: 题型:
设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足,如果直线AF的斜率为-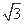 ,那么|PF|等于( )
,那么|PF|等于( )
(A)4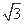 (B)8 (C)8
(B)8 (C)8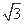 (D)16
(D)16
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线y2=4x的焦点为F,过F的直线与该抛物线相交于A(x1,y1)、B(x2,y2)两点,则 +
+ 的最小值是( )
的最小值是( )
(A)4 (B)8 (C)12 (D)16
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=xn+bx+c(n∈N+,b,c∈R).
(1)设n≥2,b=1,c=-1,证明:f(x)在区间( ,1)内存在唯一零点;
,1)内存在唯一零点;
(2)设n为偶数,|f(-1)|≤1,|f(1)|≤1,求b+3c的最小值和最大值;
(3)设n=2,若对任意x1,x2∈[-1,1],有|f(x1)-f(x2)|≤4,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,假设正确的是( )
(A)假设三个内角都不大于60度
(B)假设三个内角都大于60度
(C)假设三个内角至多有一个大于60度
(D)假设三个内角有两个大于60度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com