
(1)m为何值时,f(x)=x2+2mx+3m+4.
①有且仅有一个零点;②有两个零点且均比-1大;
(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围.
(1) ① m=4或m=-1;②(-5,-1);(2) (-4,0).
【解析】
试题分析:(1) ①由函数的零点与方程根之间的关系可知函数f(x)=x2+2mx+3m+4有且仅有一个零点,等价于方程f(x)=0有两个相等实根,而此方程是关于x的一元二次方程,所以其判别式Δ=0,从而可求得m的值;②函数f(x)=x2+2mx+3m+4有两个零点且均比-1大,结合二次函数图象可知首先其判别式应大于零,同时其对称轴应在-1的右侧,并且函数在-1的函数值大于零;从而获得一个关于m的不等式组,解此不等式组即可求得m的取值范围;(2) 函数f(x)=|4x-x2|+a有4个零点等价于|4x-x2|=-a,也即函数g(x)=|4x-x2|的图象与直线y=-a有四个不同的交点,作出图象即可求出a的取值范围.
试题解析:(1)①f(x)=x2+2mx+3m+4有且仅有一个零点,即方程f(x)=0有两个相等实根,亦即Δ=0,即4m2-4(3m+4)=0,即m2-3m-4=0,∴m=4或m=-1.
②由题意,知
即
∴-5<m<-1.
∴m的取值范围为(-5,-1).
(2)令f(x)=0,得|4x-x2|+a=0,
即|4x-x2|=-a.
令g(x)=|4x-x2|,h(x)=-a.
作出g(x)、h(x)的图象.
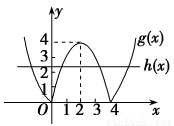
由图象可知,当0<-a<4,即-4<a<0时,g(x)与h(x)的图象有4个交点,即f(x)有4个零点.故a的取值范围为(-4,0).
考点:1.函数零点的概念;2.函数的零点与方程的根及函数图象交点之间的关系.


科目:高中数学 来源:2015届山西省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
在极坐标系中,圆ρ=-2sin θ的圆心的极坐标是( )
A.  B.
B.  C.(1,0) D.(1,π)
C.(1,0) D.(1,π)
查看答案和解析>>
科目:高中数学 来源:2015届山西省高二3月月考文科数学试卷(解析版) 题型:选择题
极坐标方程 表示的图形是( )
表示的图形是( )
A.两个圆 B.两条直线
C.一个圆和一条射线 C.一条直线和一条射线
查看答案和解析>>
科目:高中数学 来源:2015届山西大学附中高二第二学期月考理科数学试卷(解析版) 题型:选择题
设曲线 在点(1,1)处的切线与
在点(1,1)处的切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,则
,则 的值为
的值为
A.  B.
B.  C.
C.  D. 1
D. 1
查看答案和解析>>
科目:高中数学 来源:2015届山西大学附中高二第二学期月考理科数学试卷(解析版) 题型:选择题
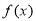 与
与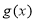 是定义在
是定义在 上的两个可导函数,若
上的两个可导函数,若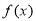 ,
,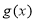 满足
满足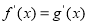 ,则
,则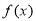 与
与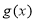 满足
满足
A.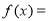
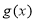 B.
B.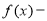
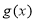 为常数函数
为常数函数
C.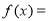
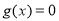 D.
D.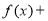
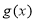 为常数函数
为常数函数
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二暑假作业数学试卷三(解析版) 题型:选择题
已知抛物线 的准线与双曲线
的准线与双曲线
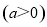 交于
交于 两点,点
两点,点 为抛物线的焦点,若
为抛物线的焦点,若 为直角三角形,则双曲线的离心率是( )
为直角三角形,则双曲线的离心率是( )
A. B.
B. C.2 D.3
C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
设函数f(x)=ax3+bx2+c,其中a+b=0,a,b,c均为常数,曲线y=f(x)在(1,f(1))处的切线方程为x+y﹣1=0.
(Ⅰ)求a,b,c的值;
(Ⅱ)求函数f(x)的单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com