
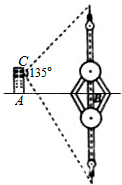
 如图所示,某人居住在离地面100米处的楼房C处,测得平静江河的对面转播塔尖以及转播塔的倒影中的塔尖的张角为135°,又知楼房离转播塔的距离AB=200m,试问:能否推算出转播塔的高度?若能,请确定塔高;若不能,请说明理由.
如图所示,某人居住在离地面100米处的楼房C处,测得平静江河的对面转播塔尖以及转播塔的倒影中的塔尖的张角为135°,又知楼房离转播塔的距离AB=200m,试问:能否推算出转播塔的高度?若能,请确定塔高;若不能,请说明理由. 分析 过C作转播塔的垂线,设转播塔高度为h,用h表示出在C处对塔尖的仰角和对塔尖倒影的俯角的正切值,使用和角的正切函数列出方程解出h.
解答 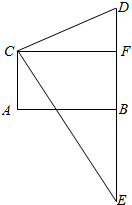 解:设转播塔尖为D,塔尖倒影为E,过C作CF⊥DE于F,则四边形ABFC是矩形,∴CF=AB=200,BF=AC=100,
解:设转播塔尖为D,塔尖倒影为E,过C作CF⊥DE于F,则四边形ABFC是矩形,∴CF=AB=200,BF=AC=100,
设传播塔高为h,则DF=h-100,EF=h+100,
∴tan∠DCF=$\frac{h-100}{200}$,tan∠ECF=$\frac{h+100}{200}$,
∵∠DCF+∠ECF=135°,
∴tan135°=$\frac{\frac{h-100}{200}+\frac{h+100}{200}}{1-\frac{h-100}{200}×\frac{h+100}{200}}$=-1.解得h=500.
∴转播塔的高度为500米.
点评 本题考查了解三角形的应用,和角的正切公式,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁大连十一中高一下学期段考二试数学(文)试卷(解析版) 题型:解答题
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:

(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三文上适应性考试一数学试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
将圆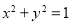 上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线
上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线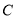 .
.
(1)写出曲线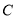 的参数方程;
的参数方程;
(2)以坐标原点为极点,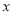 轴正半轴为极轴坐标建立极坐标系,已知直线
轴正半轴为极轴坐标建立极坐标系,已知直线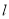 的极坐标方程为
的极坐标方程为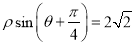 ,若
,若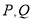 分别为曲线
分别为曲线 和直线
和直线 上的一点,求
上的一点,求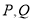 的最近距离.
的最近距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
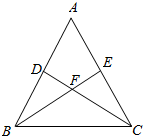 如图,在△ABC中,DC⊥AB于D,BE⊥AC于E,BE交DC于点F,若BF=FC=3,DF=FE=2.
如图,在△ABC中,DC⊥AB于D,BE⊥AC于E,BE交DC于点F,若BF=FC=3,DF=FE=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com