
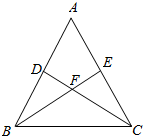
 如图,在△ABC中,DC⊥AB于D,BE⊥AC于E,BE交DC于点F,若BF=FC=3,DF=FE=2.
如图,在△ABC中,DC⊥AB于D,BE⊥AC于E,BE交DC于点F,若BF=FC=3,DF=FE=2.分析 (1)推导出B,C,D,E四点在以BC为直径的圆上,由割线定理能证明AD•AB=AE•AC.
(2)过点F作FG⊥BC于点G,推导出B,G,F,D四点共圆,F,G,C,E四点共圆,由此利用割线定理能求出BC的长.
解答 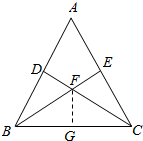 证明:(1)由已知∠BDC=∠BEC=90°,
证明:(1)由已知∠BDC=∠BEC=90°,
所以B,C,D,E四点在以BC为直径的圆上,
由割线定理知:AD•AB=AE•AC.…(3分)
解:(2)如图,过点F作FG⊥BC于点G,
由已知,∠BDC=90°,又因为FG⊥BC,所以B,G,F,D四点共圆,
所以由割线定理知:CG•CB=CF•CD,①…(5分)
同理,F,G,C,E四点共圆,由割线定理知:
BF•BE=BG•BC,②…(7分)
①+②得:CG•CB+BG•BC=CF•CD+BF•BE,
即BC2=CF•CD+BF•BE=3×5+3×5=30,…(8分)
所以BC=$\sqrt{30}$.…(10分)
点评 本题考查两组线段长的乘积相等的证明,考查线段长的求法,是中档题,解题时要认真审题,注意四点共圆和切割线定理的合理运用.


科目:高中数学 来源: 题型:解答题
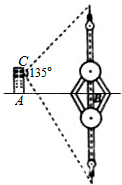 如图所示,某人居住在离地面100米处的楼房C处,测得平静江河的对面转播塔尖以及转播塔的倒影中的塔尖的张角为135°,又知楼房离转播塔的距离AB=200m,试问:能否推算出转播塔的高度?若能,请确定塔高;若不能,请说明理由.
如图所示,某人居住在离地面100米处的楼房C处,测得平静江河的对面转播塔尖以及转播塔的倒影中的塔尖的张角为135°,又知楼房离转播塔的距离AB=200m,试问:能否推算出转播塔的高度?若能,请确定塔高;若不能,请说明理由.查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三文上适应性考试一数学试卷(解析版) 题型:解答题
已知函数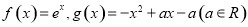 ,点
,点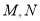 分别在
分别在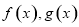 的图象上.
的图象上.
(1)若函数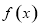 在
在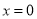 处的切线恰好与
处的切线恰好与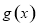 相切,求
相切,求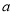 的值;
的值;
(2)若点 的横坐标均为
的横坐标均为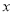 ,记
,记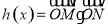 ,当
,当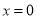 时,函数
时,函数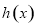 取得极大值,求
取得极大值,求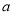 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{6}$ | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4+$\sqrt{17}$ | B. | 3+$2\sqrt{5}$ | C. | $\frac{19}{2}$ | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
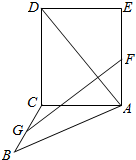 如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点,求
如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点,求查看答案和解析>>
科目:高中数学 来源: 题型:解答题
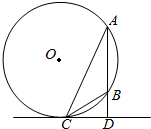 如图,A、B是圆O上的两点,且AB的长度小于圆O的直径,直线l与AB垂于点D且与圆O相切于点C.若AB=2,DB=1
如图,A、B是圆O上的两点,且AB的长度小于圆O的直径,直线l与AB垂于点D且与圆O相切于点C.若AB=2,DB=1查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4件都是正品 | B. | 至少有一件次品 | C. | 4件都是次品 | D. | 至少有一件正品 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com