
分析 利用双曲线的定义,确定△APF周长最小时,P的坐标,即可求出△APF周长最小时,该三角形的面积
解答 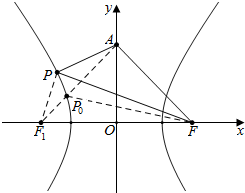 解:设左焦点为F1(-2,0),右焦点为F(2,0).
解:设左焦点为F1(-2,0),右焦点为F(2,0).
△APF周长为|AF|+|AP|+|PF|=|AF|+|AP|+(|PF1|+2a)=|AF|+|AP|+|PF1|+2a≥|AF|+|AF1|+2a,
当且仅当A,P,F1三点共线,即P位于P0时,三角形周长最小.
此时直线AF1的方程为y=x+2,代入x2-y2=2中,可求得${P_0}({-\frac{3}{2},\frac{1}{2}})$,
故${S_{△A{P_0}F}}={S_{△A{F_1}F}}-{S_{△{P_0}{F_1}F}}=\frac{1}{2}×4×2-\frac{1}{2}×4×\frac{1}{2}=3$.
故答案为:3.
点评 本题考查双曲线的定义,考查三角形面积的计算,确定P的坐标是关键.


科目:高中数学 来源:2017届重庆市高三文上适应性考试一数学试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
将圆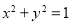 上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线
上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线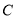 .
.
(1)写出曲线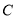 的参数方程;
的参数方程;
(2)以坐标原点为极点,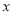 轴正半轴为极轴坐标建立极坐标系,已知直线
轴正半轴为极轴坐标建立极坐标系,已知直线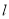 的极坐标方程为
的极坐标方程为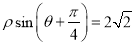 ,若
,若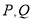 分别为曲线
分别为曲线 和直线
和直线 上的一点,求
上的一点,求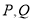 的最近距离.
的最近距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
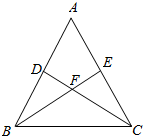 如图,在△ABC中,DC⊥AB于D,BE⊥AC于E,BE交DC于点F,若BF=FC=3,DF=FE=2.
如图,在△ABC中,DC⊥AB于D,BE⊥AC于E,BE交DC于点F,若BF=FC=3,DF=FE=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
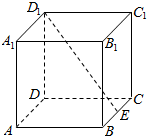 如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )
如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )| A. | $\frac{{4\sqrt{5}}}{5}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
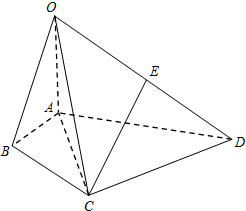 如图,在四棱锥O-ABCD中,∠BAD=120°,OA⊥平面ABCD,E为OD的中点,OA=AC=$\frac{1}{2}$AD=2,AC平分∠BAD.
如图,在四棱锥O-ABCD中,∠BAD=120°,OA⊥平面ABCD,E为OD的中点,OA=AC=$\frac{1}{2}$AD=2,AC平分∠BAD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
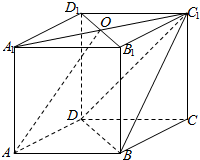 在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1与B1D1的交点,已知AA1=AB=1,∠BAD=60°.
在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1与B1D1的交点,已知AA1=AB=1,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
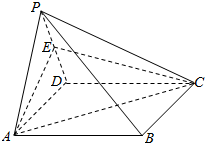 已知四棱锥P-ABCD的底面ABCD是矩形,PD⊥底面ABCD,E为棱PD的中点.
已知四棱锥P-ABCD的底面ABCD是矩形,PD⊥底面ABCD,E为棱PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
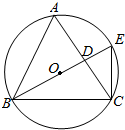 如图,点E在△ABC的外接圆O上,AB=AC,$\widehat{AE}$=$\widehat{CE}$,AC交BE于点D,圆O的面积为S.
如图,点E在△ABC的外接圆O上,AB=AC,$\widehat{AE}$=$\widehat{CE}$,AC交BE于点D,圆O的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
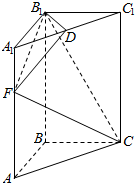 如图,高为3的直三棱柱ABC-A1B1C1中,底面是直角三角形,AC=2,D为A1C1的中点,F在线段AA1上,CF⊥DB1,且A1F=1.
如图,高为3的直三棱柱ABC-A1B1C1中,底面是直角三角形,AC=2,D为A1C1的中点,F在线段AA1上,CF⊥DB1,且A1F=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com