练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．已知f（x）=-x2+10，则f（x）在x=$\frac{3}{2}$处的瞬时变化率是（　　）
    A．3B．-3C．2D．-2

    分析 根据导数的物理意义求函数的导数即可．

    解答 解：∵f（x）=-x2+10，
    ∴f′（x）=-2x，
    即当x=$\frac{3}{2}$时，f′（$\frac{3}{2}$）=-3，
    即在点x=$\frac{3}{2}$处的瞬时变化率是-3，
    故选：B．

    点评 本题主要考查导数的物理意义的应用，求函数的导数解决本题的关键．比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    1．根据下列条件，求相应的等差数列{an}的有关未知数：
    （1）a1=20，an=54，Sn=999．求d及n；
    （2）d=$\frac{1}{3}$，n=37，Sn=629，求a1及an；
    （3）a1=$\frac{5}{6}$，d=-$\frac{1}{6}$，Sn=-5，求n及an；
    （4）d=2，n=15，an=-10，求a1及Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．在△ABC中，A，B，C角对边分别为a，b，c．且3acosB=bcosC+ccosB．
    （1）求sinB的值．
    （2）若b=4，且a=c，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．化简：1!+2•2!+3•3!+…+n•n!

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知命题p：?m∈R，使得函数f（x）=x3+（m-1）x2-2是奇函数，命题q：向量$\overrightarrow{a}$=（x1，y1），$\overrightarrow{b}$=（x2，y2），则“$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$”是：“$\overrightarrow{a}$∥$\overrightarrow{b}$”的充要条件，则下列命题为真命题的是（　　）
    A．p∧qB．（￢p）∧qC．p∧（￢q）D．（￢p）∧（￢q）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知点A（2，1，1），B（0，1，-1），C（1，0，1），试找出平面ABC的-个法向量．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知曲线y=x2在点P处的切线分别满足下列条件，求点P坐标．
    （1）平行于直线y=4x-5；
    （2）与x轴成135°的倾斜角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．设复数z的共轭复数为$\overline{z}$，且4z+2$\overline{z}$=3$\sqrt{3}$+i，ω=sinθ-icosθ，复数z-ω对应复平面内的向量为$\overrightarrow{OM}$，求复数z和|$\overrightarrow{OM}$|的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

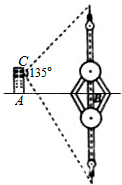    1．如图所示，某人居住在离地面100米处的楼房C处，测得平静江河的对面转播塔尖以及转播塔的倒影中的塔尖的张角为135°，又知楼房离转播塔的距离AB=200m，试问：能否推算出转播塔的高度？若能，请确定塔高；若不能，请说明理由．

    查看答案和解析>>

    同步练习册答案