
分析 设出复数z的形式,由题意和复数相等可得方程组,解方程组可得z,再由模长公式和三角函数可得.
解答 解:设z=a+bi,a,b∈R,则$\overline{z}$=a-bi,
代入且4z+2$\overline{z}$=3$\sqrt{3}$+i可得4a+4bi+2a-2bi=3$\sqrt{3}$+i,
化简可得6a+2bi=3$\sqrt{3}$+i,
由复数相等可得6a=3$\sqrt{3}$,2b=1,
解得a=$\frac{\sqrt{3}}{2}$,b=$\frac{1}{2}$,∴z=$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$i,
∴|$\overrightarrow{OM}$|=|z-ω|=|($\frac{\sqrt{3}}{2}$-sinθ)+($\frac{1}{2}$+cosθ)i|
=$\sqrt{(\frac{\sqrt{3}}{2}-sinθ)^{2}+(\frac{1}{2}+cosθ)^{2}}$
=$\sqrt{2-\sqrt{3}sinθ+cosθ}$
=$\sqrt{2-2sin(θ-\frac{π}{6})}$,
∵-1≤sin($θ-\frac{π}{6}$)≤1,
∴0≤2-2sin($θ-\frac{π}{6}$)≤4,
∴0≤|$\overrightarrow{OM}$|≤2
点评 本题考查复数相等和模长,涉及三角函数公式和三角函数的值域,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+b≥2($\sqrt{2}$+1) | B. | a+b≤$\sqrt{2}$+1 | C. | a+b≤($\sqrt{2}$+1)2 | D. | a+b>2($\sqrt{2}$+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 120种 | B. | 240种 | C. | 320种 | D. | 625种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三文上适应性考试一数学试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
将圆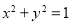 上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线
上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线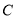 .
.
(1)写出曲线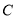 的参数方程;
的参数方程;
(2)以坐标原点为极点,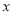 轴正半轴为极轴坐标建立极坐标系,已知直线
轴正半轴为极轴坐标建立极坐标系,已知直线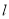 的极坐标方程为
的极坐标方程为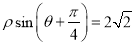 ,若
,若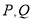 分别为曲线
分别为曲线 和直线
和直线 上的一点,求
上的一点,求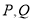 的最近距离.
的最近距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com