
分析 由平面向量的坐标运算求出$\overrightarrow{μ}$=$\overrightarrow{a}$+t$\overrightarrow{b}$的坐标,求模后利用二次函数求最值.
解答 解:∵$\overrightarrow{a}$=(cos25°,sin25°)$\overrightarrow{b}$=(sin20°,cos20°),
∴$\overrightarrow{μ}$=$\overrightarrow{a}$+t$\overrightarrow{b}$=(cos25°,sin25°)+t(sin20°,cos20°)=(cos25°+tsin20°,sin25°+tcos20°),
则|$\overrightarrow{μ}$|=$\sqrt{(cos25°+tsin20°)^{2}+(sin25°+tcos20°)^{2}}$
=$\sqrt{1+{t}^{2}+2t•sin45°}$=$\sqrt{{t}^{2}+\sqrt{2}t+1}$,
∴当t=$-\frac{\sqrt{2}}{2}$时,|$\overrightarrow{μ}$|有最小值为$\sqrt{(-\frac{\sqrt{2}}{2})^{2}+\sqrt{2}×(-\frac{\sqrt{2}}{2})+1}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查平面向量的坐标运算,考查了向量模的求法,是基础题.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -2$\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
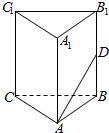 如图所示,在正三棱柱ABC-A1B1C1中,已知AB=1,D是棱BB1上的点,且BD=1,求:
如图所示,在正三棱柱ABC-A1B1C1中,已知AB=1,D是棱BB1上的点,且BD=1,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com