
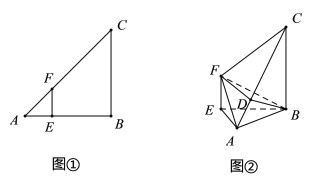
【题目】如图①,在![]() 中,
中,![]() 为直角,
为直角,![]() ,
,![]() ,
,![]() ,沿
,沿![]() 将
将![]() 折起,使
折起,使![]() ,得到如图②的几何体,点
,得到如图②的几何体,点![]() 在线段
在线段![]() 上.
上.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由余弦定理得出![]() ,进而得出
,进而得出![]() ;由
;由![]() 平面
平面![]() ,得出
,得出![]() ;从而得到
;从而得到![]() 平面
平面![]() ,即可证明平面
,即可证明平面![]() 平面
平面![]() .
.
(2)建立空间直角坐标系,求得平面![]() 的法向量,即可求得直线
的法向量,即可求得直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)证明:在![]() 中,
中,
∵![]() ,
,![]() ,
,![]() ,
,
由余弦定理得![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() ,
,
又![]() ,
,![]() 平面
平面![]() ∴
∴![]() 平面
平面![]()
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]()
(2)解法一:
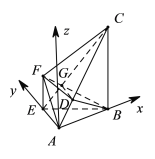
如图,以![]() 为原点,以
为原点,以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过点
轴,过点![]() 垂直于平面
垂直于平面![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系,如图所示:
轴,建立空间直角坐标系,如图所示:
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]()
连结![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 为平面
为平面![]() 与平面
与平面![]() 的交线,
的交线,
∴![]() ,∴
,∴![]() ,
,
在四边形![]() 中,∵
中,∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
设![]() ,则
,则![]() ,
,
由![]() ,得
,得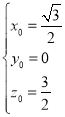 ,∴
,∴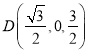 ,∴
,∴
设平面![]() 的法向量为
的法向量为![]() ,
,
则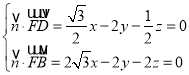 ,取
,取![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则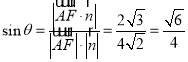 .
.
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(2)解法二:
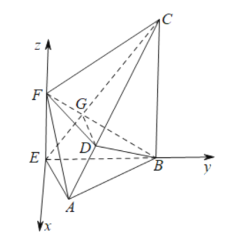
如图,以![]() 为原点,在平面
为原点,在平面![]() 中过
中过![]() 作
作![]() 的垂线为
的垂线为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,如图所示:
轴,建立空间直角坐标系,如图所示:
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]()
连结![]() ,与
,与![]() 交于点
交于点![]() ,连结
,连结![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 为平面
为平面![]() 与平面
与平面![]() 的交线,
的交线,
∴![]() ,∴
,∴![]() ,
,
在四边形![]() 中,∴
中,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
由![]() 得:
得: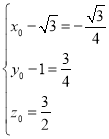 解得
解得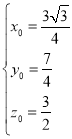 ,∴
,∴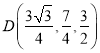 ,
,
∴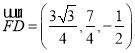 .
.
设平面的法向量![]() ,
,
则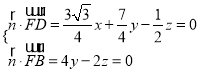 ,取
,取![]() ,则
,则![]() ,
,![]() ,
,
∴ ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则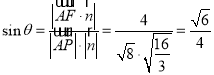 .
.
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左焦点
的左焦点![]() ,点
,点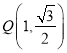 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)经过圆![]() :
:![]() 上一动点
上一动点![]() 作椭圆
作椭圆![]() 的两条切线,切点分别记为
的两条切线,切点分别记为![]() ,
,![]() ,直线
,直线![]() ,
,![]() 分别与圆
分别与圆![]() 相交于异于点
相交于异于点![]() 的
的![]() ,
,![]() 两点.
两点.
(i)求证:![]() ;
;
(ii)求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为梯形,
为梯形, ![]() ,且
,且![]() ,
, ![]() 是边长为2的正三角形,顶点
是边长为2的正三角形,顶点![]() 在
在![]() 上的射影为点
上的射影为点![]() ,且
,且![]() ,
, ![]() ,
, ![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)求曲线![]() 的直角坐标方程与直线l的参数方程;
的直角坐标方程与直线l的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间用一台包装机包装葡萄糖,每袋葡萄糖的重量是一个随机变量,它服从正态分布.当机器工作正常时,每袋葡萄糖平均重量![]() 为0.5kg,标准差
为0.5kg,标准差![]() 为0.015kg.
为0.015kg.
(1)已知包装每袋葡萄糖的成本为1元,若发现包装好的葡萄糖重量异常,则需要将该袋葡萄糖进行重新包装,假设重新包装后的葡萄糖重量正常.若某袋葡萄糖的重量![]() 满足
满足![]() ,则认为该袋葡萄糖重量正常. 问:在机器工作正常的情况下,至少包装多少袋葡萄糖才能使“至少有一袋包装好的葡萄糖重量正常”的概率大于0.98?并求出相应成本的最小期望值.
,则认为该袋葡萄糖重量正常. 问:在机器工作正常的情况下,至少包装多少袋葡萄糖才能使“至少有一袋包装好的葡萄糖重量正常”的概率大于0.98?并求出相应成本的最小期望值.
(2)某日开工后, 为检査该包装机工作是否正常, 随机地抽取它所包装的葡萄糖9袋,若抽取的9袋葡萄糖称得净重(kg)为:0.496, 0.508, 0.524, 0.519, 0.495, 0.510, 0.522, 0.513, 0.512.用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,以
,以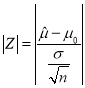 作为检验统计量,其中
作为检验统计量,其中![]() 为样本总数,
为样本总数,![]() 服从正态分布
服从正态分布![]() ,且
,且![]() .
.
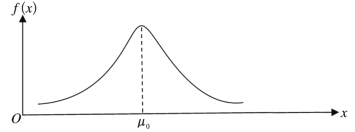
①若机器工作正常时, 每袋葡萄糖的重量服从的正态分布曲线如下图所示,且经计算得上述样本数据的标准差![]() 0.022.请在下图(机器正常工作时的正态分布曲线)中,绘制出以该样本作为估计得到的每袋葡萄糖所服从的正态分布曲线的草图.
0.022.请在下图(机器正常工作时的正态分布曲线)中,绘制出以该样本作为估计得到的每袋葡萄糖所服从的正态分布曲线的草图.
②若![]() ,就推断该包装机工作异常,这种推断犯错误的概率不超过
,就推断该包装机工作异常,这种推断犯错误的概率不超过![]() ,试以95%的可靠性估计该包装机工作是否正常.
,试以95%的可靠性估计该包装机工作是否正常.
附: 若随机变量![]() 服从正态分布:
服从正态分布:![]() ,
,![]()
![]()
参考数据:![]() ;
;![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设点![]() 的坐标分别为
的坐标分别为![]() ,直线
,直线![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() .
.
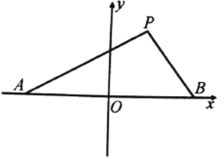
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为
的轨迹为![]() ,点
,点![]() 是轨迹为
是轨迹为![]() 上不同于
上不同于![]() 的两点,且满足
的两点,且满足![]() ,求证:
,求证:![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是抛物线
是抛物线![]() 上的两个不同的点,
上的两个不同的点,![]() 是坐标原点.若直线
是坐标原点.若直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,则( ).
,则( ).
A.![]() B.以
B.以![]() 为直径的圆的面积大于
为直径的圆的面积大于![]()
C.直线![]() 过定点
过定点![]() D.点
D.点![]() 到直线
到直线![]() 的距离不大于2
的距离不大于2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商家通常依据“乐观系数准则”确定商品销售价格,及根据商品的最低销售限价a,最高销售限价b(b>a)以及常数x(0<x<1)确定实际销售价格c=a+x(b﹣a),这里,x被称为乐观系数.
经验表明,最佳乐观系数x恰好使得(c﹣a)是(b﹣c)和(b﹣a)的等比中项,据此可得,最佳乐观系数x的值等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com