
 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:解答题
(本题满分12分)号码为1、2、3、4、5、6的六个大小相同的球,放入编号为1、2、3、4、5、6的六个盒子中,每个盒子只能放一个球.
(Ⅰ)若1号球只能放在1号盒子中,2号球只能放在2号的盒子中,则不同的放法有多少种?
(Ⅱ)若3号球只能放在1号或2号盒子中,4号球不能放在4号盒子中,则不同的放法有多少种?
(Ⅲ)若5、6号球只能放入号码是相邻数字的两个盒子中,则不同的放法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
5个人排成一排,按下列要求各有多少种不同的排法?
(1)其中甲不站排头,乙不站排尾;
(2)其中甲、乙2人必须相邻;
(3)其中甲、乙2人不能相邻;
(4)其中甲、乙中间有且只有1人;
(5)其中甲只能站在乙的左侧.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有7名同学去参加一个活动,分别求出以下不同要求的方法数(以下各小题写出必要的计算公式,最终结果用数字作答)
(1)排队时7名同学中的丙不站在中间的排法
(2)排队时7名同学中的甲、乙、丙三名同学各不相邻的排法
(3)排队时7名同学中的甲不能站在最前并且已不能站在最后的排法(理科学生做)
(4)7名学生选出3名代表发言,甲,乙,丙三名同学至多两人个入选的选法(理科学生做)
7名学生中选出3名代表发言,甲、乙只有一人入选的选法有多少?(文科学生做)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)从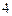 名男同学中选出
名男同学中选出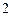 人,
人, 名女同学中选出
名女同学中选出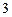 人,并将选出的
人,并将选出的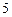 人排成一排.
人排成一排.
(1)共有多少种不同的排法?
(2)若选出的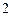 名男同学不相邻,共有多少种不同的排法?(用数字表示)
名男同学不相邻,共有多少种不同的排法?(用数字表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com