
分析 由题意转化为方程f(x)=(3x-1)($\sqrt{9{x}^{2}-6x+5}$+1)+(2x-3)($\sqrt{4{x}^{2}-12x+13}$+1)=0的解,从而可得(3x-1)($\sqrt{(3x-1)^{2}+4}$+1)=(3-2x)($\sqrt{(3-2x)^{2}+4}$+1),再令g(x)=x($\sqrt{{x}^{2}+4}$+1),从而求导以判断函数的单调性,从而解得.
解答 解:由题意,
令f(x)=(3x-1)($\sqrt{9{x}^{2}-6x+5}$+1)+(2x-3)($\sqrt{4{x}^{2}-12x+13}$+1)=0,
即(3x-1)($\sqrt{(3x-1)^{2}+4}$+1)=(3-2x)($\sqrt{(3-2x)^{2}+4}$+1),
令g(x)=x($\sqrt{{x}^{2}+4}$+1),g′(x)=$\sqrt{{x}^{2}+4}$+1+$\frac{{x}^{2}}{\sqrt{{x}^{2}+4}}$>0,
故g(x)=x($\sqrt{{x}^{2}+4}$+1)在R上单调递增;
故3x-1=3-2x,
解得,x=$\frac{4}{5}$;
故答案为:($\frac{4}{5}$,0).
点评 本题考查了导数的综合应用及函数与方程的关系应用.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
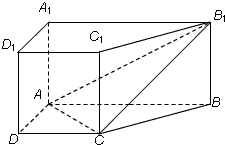 直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2,侧棱长为1.
直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2,侧棱长为1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,4+2$\sqrt{2}$] | B. | [$\frac{3}{2}$,7] | C. | [$\frac{3}{2}$,4+2$\sqrt{2}$] | D. | [4-2$\sqrt{2}$,7] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com