Question

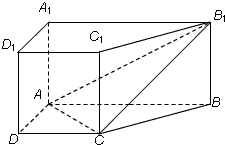
20．直棱柱ABCD-A₁B₁C₁D₁中，底面ABCD是直角梯形，∠BAD=∠ADC=90°，AB=2AD=2CD=2，侧棱长为1．
（1）建立适当的空间直角坐标系，并写出点A、C、B₁的坐标．
（2）判断△ACB₁是否为直角三角形？证明你的结论．

Answer 1

分析 （1）以A为原点，分别以AB，AD，AA₁所在直线为x，y，z轴建立空间直角坐标系，得到各点的坐标；
（2）利用（1）的结论得到△ACB₁的三边对应的向量，利用数量积是否为0，判断三角形是否是直角三角形．

解答 解：（1）以A为原点，分别以AB，AD，AA₁所在直线为x，y，z轴建立空间直角坐标系，如图，

则A（0，0，0），C（1，1，0），B₁（2，0，1）；
（2）△ACB₁为直角三角形；
证明：由（1）可知$\overrightarrow{AC}$=（1，1，0），$\overrightarrow{A{B}_{1}}$=（2，0，1），$\overrightarrow{C{B}_{1}}$=（1，-1，1），所以$\overrightarrow{AC}•\overrightarrow{C{B}_{1}}$=0，所以$\overrightarrow{AC}⊥\overrightarrow{C{B}_{1}}$，
所以△ACB₁为直角三角形．

点评 本题考查了利用空间向量解决空间直线的位置关系、判断三角形的形状；关键是正确建立空间直角坐标系，使问题向量化．