
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
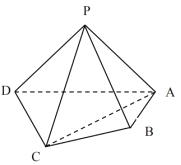
(1)求证:![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的线面角的正弦值为
所成的线面角的正弦值为![]() ,求
,求![]() 长.
长.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左顶点
,左顶点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若以
两点,若以![]() 为直径的圆经过坐标原点,证明:
为直径的圆经过坐标原点,证明:![]() 到直线
到直线![]() 的距离为定值.
的距离为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个工厂生产某种产品每年需要固定投资100万元,此外每生产1件该产品还需要增加投资1万元,年产量为![]() (
(![]() )件.当
)件.当![]() 时,年销售总收人为(
时,年销售总收人为(![]() )万元;当
)万元;当![]() 时,年销售总收人为
时,年销售总收人为![]() 万元.记该工厂生产并销售这种产品所得的年利润为
万元.记该工厂生产并销售这种产品所得的年利润为![]() 万元.(年利润=年销售总收入一年总投资)
万元.(年利润=年销售总收入一年总投资)
(1)求![]() (万元)与
(万元)与![]() (件)的函数关系式;
(件)的函数关系式;
(2)当该工厂的年产量为多少件时,所得年利润最大?最大年利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
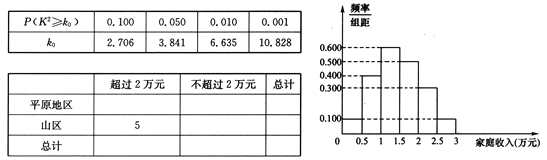
【题目】某贫困地区有1500户居民,其中平原地区1050户,山区450户.为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据(单位:万元).
(Ⅰ)应收集多少户山区家庭的样本数据?
(Ⅱ)根据这150个样本数据,得到2017年家庭收入的频率分布直方图(如图所示),其中样本数据分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
.如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
(Ⅲ)样本数据中,由5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有![]() 的把握认为“该地区2017年家庭年收入与地区有关”?
的把握认为“该地区2017年家庭年收入与地区有关”?
附:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】①函数y=cos(![]() x+
x+![]() )是奇函数;
)是奇函数;
②存在实数![]() ,使得sin
,使得sin![]() +cos
+cos![]() =2;
=2;
③若![]() 、
、![]() 是第一象限角且
是第一象限角且![]() <
<![]() ,则tan
,则tan![]() <tan
<tan![]() ;
;
④x=![]() 是函数y=sin(2x+
是函数y=sin(2x+![]() )的一条对称轴方程;
)的一条对称轴方程;
⑤函数y=tan(2x+![]() )的图象关于点(
)的图象关于点(![]() ,0)成中心对称图形.
,0)成中心对称图形.
其中正确命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面上,称横、纵坐标都是有理数的点为有理点.求满足如下条件的最小正整数![]() :每一个圆周上含有
:每一个圆周上含有![]() 个有理点的圆,它的圆周上一定含有无穷多个有理点.
个有理点的圆,它的圆周上一定含有无穷多个有理点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2-(2m+1)x+m.
(1)若方程f(x)=0有两个不等的实根x1,x2,且-1<x1<0<x2<1,求m的取值范围;
(2)若对任意的x∈[1,2],![]() ≤2恒成立,求m的取值范围.
≤2恒成立,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com