
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左顶点
,左顶点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若以
两点,若以![]() 为直径的圆经过坐标原点,证明:
为直径的圆经过坐标原点,证明:![]() 到直线
到直线![]() 的距离为定值.
的距离为定值.
【答案】(1)![]() .(2)见解析
.(2)见解析
【解析】
(1)结合离心率![]() ,计算出a,b,c之间的关系,利用点到直线距离,计算a,b值,即可。(2)分直线AB斜率存在与不存在讨论,结合直线方程和椭圆方程,并利用
,计算出a,b,c之间的关系,利用点到直线距离,计算a,b值,即可。(2)分直线AB斜率存在与不存在讨论,结合直线方程和椭圆方程,并利用![]() ,计算O到直线距离,即可.
,计算O到直线距离,即可.
(1)∵椭圆![]() 的离心率
的离心率![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∵椭圆![]() 的左顶点
的左顶点![]() 到直线
到直线![]() ,即到
,即到![]() 的距离
的距离![]() ,
,
∴![]() ,
,
把![]() 代入得:
代入得:![]() ,解得:
,解得:![]() ,
,
∴![]() ,
,![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
,
①当直线![]() 的斜率不存在时,由椭圆的性质可得:
的斜率不存在时,由椭圆的性质可得:![]() ,
,![]() ,
,
∵当直线![]() 的斜率不存在时,以
的斜率不存在时,以![]() 为直径的圆经过坐标原点,
为直径的圆经过坐标原点,
∴![]() ,即
,即![]() ,也就是
,也就是![]() ,
,
又∵点![]() 在椭圆
在椭圆![]() 上, ∴
上, ∴![]() ,
,
∵以![]() 为直径的圆经过坐标原点,且
为直径的圆经过坐标原点,且![]() 平行于
平行于![]() 轴,
轴,
∴![]() ,∴
,∴![]() ,解得:
,解得:![]()
此时点![]() 到直线
到直线![]() 的距离
的距离![]()
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
与椭圆方程联立有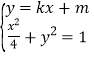 ,消去
,消去![]() ,得
,得![]()
∴![]() ,
,![]() ,
,
同理: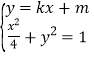 ,消去
,消去![]() ,得
,得![]() ,
,
即![]() ,∴
,∴![]()
∵![]() 为直径的圆过坐标原点
为直径的圆过坐标原点![]() ,所以
,所以![]() ,∴
,∴![]()
∴![]()
∴![]()
∴![]()
∴点![]() 到直线
到直线![]() 的距离
的距离![]()
综上所述,点![]() 到直线
到直线![]() 的距离为定值
的距离为定值![]() .
.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量![]() (件)与单价
(件)与单价![]() (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.

(1)根据周销售量图写出![]() (件)与单价
(件)与单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)写出利润![]() (元)与单价
(元)与单价![]() (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
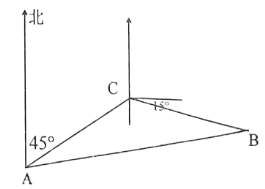
【题目】宿州泗县石龙湖国家湿地公园是保存完好的典型湿地生态系统,具有得天独厚的旅游资源.某日一游船在湖上游玩航行中突然遇险,发出呼救信号,驻湖救援队在![]() 处获悉后,立即测出该游船在北偏东
处获悉后,立即测出该游船在北偏东![]() 方向上,距离
方向上,距离![]() 有
有![]() 千米的
千米的![]() 处,并测得游船正沿东偏南
处,并测得游船正沿东偏南![]() 的方向,以
的方向,以![]() 千米/时的速度向湖心小岛
千米/时的速度向湖心小岛![]() 靠拢,救援舰艇立即以
靠拢,救援舰艇立即以![]() 千米/时的速度前去营救,若想用最短的时间营救游船,求舰艇的航行方向和所需时间.
千米/时的速度前去营救,若想用最短的时间营救游船,求舰艇的航行方向和所需时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() .若满射
.若满射![]() ,满足:对任意的
,满足:对任意的![]() ,
,![]() ,则称
,则称![]() 为“和谐函数”.记
为“和谐函数”.记 ![]() ,
,![]() .设“和谐映射”
.设“和谐映射”![]() 为满足条件:存在正整数
为满足条件:存在正整数![]() ,使得(1)当
,使得(1)当![]() 时,若
时,若![]() ,
,![]() ,则
,则![]()
![]()
![]() ;(2)若
;(2)若![]() ,
,![]() ,则
,则![]() ,求
,求![]() 的最大可能值.
的最大可能值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种排卡游戏规则如下:将写有![]() 的九张卡片随机地排成一行,第一张卡片:左起)上的标数为
的九张卡片随机地排成一行,第一张卡片:左起)上的标数为![]() ,则将前
,则将前![]() 张卡片逆序排过来称为一次操作,无法操作时(即第一张卡片上的标数“1”)游戏停止.若一个排列无法操作,且恰由唯一的另一个排列经过一次操作得到,则此排列称为“二次终止排列”.在所有可能的排列中,求二次终止排列出现的概率.
张卡片逆序排过来称为一次操作,无法操作时(即第一张卡片上的标数“1”)游戏停止.若一个排列无法操作,且恰由唯一的另一个排列经过一次操作得到,则此排列称为“二次终止排列”.在所有可能的排列中,求二次终止排列出现的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有5个匣子,每个匣子有一把钥匙,并且钥匙不能通用.如果随意在每一个匣内放入一把钥匙,然后把匣子全都锁上.现在允许砸开一个匣子,使得能相继用钥匙打开其余4个匣子,那么钥匙的放法有______种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,其中
,其中![]() ,
,![]() 是函数
是函数![]() 定义城内任意不相等的两个实数.
定义城内任意不相等的两个实数.
(1)若![]() ,同时
,同时![]() ,求证:
,求证:![]() ;
;
(2)判断![]() 是否在集合A中,并说明理由;
是否在集合A中,并说明理由;
(3)设函数![]() 的定义域为B,函数
的定义域为B,函数![]() 的值域为C.函数
的值域为C.函数![]() 满足以下3个条件:
满足以下3个条件:
①![]() ,②
,②![]() ,③
,③![]() .试确定一个满足以上3个条件的函数
.试确定一个满足以上3个条件的函数![]() 要对满足的条件进行说明).
要对满足的条件进行说明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com