
【题目】某贫困地区有1500户居民,其中平原地区1050户,山区450户.为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据(单位:万元).
(Ⅰ)应收集多少户山区家庭的样本数据?
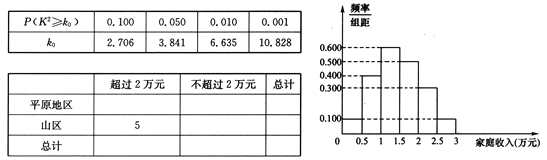
(Ⅱ)根据这150个样本数据,得到2017年家庭收入的频率分布直方图(如图所示),其中样本数据分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
.如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
(Ⅲ)样本数据中,由5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有![]() 的把握认为“该地区2017年家庭年收入与地区有关”?
的把握认为“该地区2017年家庭年收入与地区有关”?
附:![]()
【答案】(Ⅰ)45;(Ⅱ)![]() ;(Ⅲ)有
;(Ⅲ)有![]() 的把握认为“该地区2017年家庭年收入与地区有关”.
的把握认为“该地区2017年家庭年收入与地区有关”.
【解析】分析:(Ⅰ)利用分层抽样中每层所抽取的比例数相等求得答案;(Ⅱ)根据频率分布直方图可得该地区2017年家庭收入超过1.5万元的概率;(Ⅲ)由题意列出2×2列联表,计算出![]() 的值,结合附表得答案.
的值,结合附表得答案.
详解:(Ⅰ)由已知可得每户居民被抽取的概率为0.1,故应手机![]() 户山区家庭的样本数据.
户山区家庭的样本数据.
(Ⅱ)由直方图可知该地区2017年家庭年收入超过1.5万元的概率约为![]() .
.
(Ⅲ)样本数据中,年收入超过2万元的户数为![]() 户.
户.
而样本数据中,有5户山区家庭的年收入超过2万元,故列联表如下:

所以![]() ,
,
∴有![]() 的把握认为“该地区2017年家庭年收入与地区有关”.
的把握认为“该地区2017年家庭年收入与地区有关”.


科目:高中数学 来源: 题型:
【题目】设A,B,C,D为平面内的四点,且A(1,3),B(2,–2),C(4,1).
(1)若![]() ,求D点的坐标;
,求D点的坐标;
(2)设向量![]() ,
,![]() ,若k
,若k![]() –
–![]() 与
与![]() +3
+3![]() 平行,求实数
平行,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
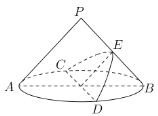
【题目】我们知道:用平行于圆锥母线的平面(不过顶点)截圆锥,则平面与圆锥侧面的交线是抛物线一部分,如图,在底面半径和高均为2的圆锥中,![]()
![]() 是底面圆
是底面圆![]() 的两条互相垂直的直径,
的两条互相垂直的直径,![]() 是母线
是母线![]() 的中点,已知过
的中点,已知过![]() 与
与![]() 的平面与圆锥侧面的交线是以
的平面与圆锥侧面的交线是以![]() 为顶点的圆锥曲线的一部分,则该圆锥曲线的焦点到其准线的距离等于__________.
为顶点的圆锥曲线的一部分,则该圆锥曲线的焦点到其准线的距离等于__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 学校有15位数学老师,其中9位男老师,6位女老师,
学校有15位数学老师,其中9位男老师,6位女老师,![]() 学校有10位数学老师,其中3位男老师,7位女老师,为了实现师资均衡,现从
学校有10位数学老师,其中3位男老师,7位女老师,为了实现师资均衡,现从![]() 学校任意抽取一位数学老师到
学校任意抽取一位数学老师到![]() 学校,然后从
学校,然后从![]() 学校随机抽取一位数学老师到市里上公开课,则在
学校随机抽取一位数学老师到市里上公开课,则在![]() 学校抽到
学校抽到![]() 学校的老师是男老师的情况下,从
学校的老师是男老师的情况下,从![]() 学校抽取到市里上公开课的也是男老师的概率是( )
学校抽取到市里上公开课的也是男老师的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只红铃虫的产卵数![]() 和温度
和温度![]() 有关,现收集了4组观测数据列于下表中,根据数据作出散点图如下:
有关,现收集了4组观测数据列于下表中,根据数据作出散点图如下:
温度 | 20 | 25 | 30 | 35 |
产卵数 | 5 | 20 | 100 | 325 |

参考数据:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,
![]() ,
,![]()
| 5 | 20 | 100 | 325 |
| 1.61 | 3 | 4.61 | 5.78 |
(1)根据散点图判断![]() 与
与![]() 哪一个更适宜作为产卵数
哪一个更适宜作为产卵数![]() 关于温度
关于温度![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(数字保留2位小数);
的回归方程(数字保留2位小数);
(3)要使得产卵数不超过50,则温度控制在多少![]() 以下?(最后结果保留到整数)
以下?(最后结果保留到整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com