练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设A，B，C，D为平面内的四点，且A（1，3），B（2，–2），C（4，1）．

    （1）若，求D点的坐标；

    （2）设向量，，若k–与+3平行，求实数 的值．

    【答案】（1）D（5，–4）；（2）k=–．

    【解析】

    （1）设D（x，y），

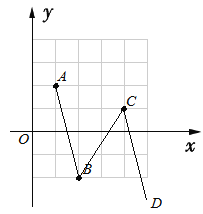
    ∵A，B，C，D为平面内的四点，且A（1，3），B（2，–2），C（4，1）．如图，

    ∴由，得（2，–2）–（1，3）=（x，y）–（4，1），

    即（1，–5）=（x–4，y–1），

    ∴，解得x=5，y=–4，∴D（5，–4）．

    （2）∵=（1，–5），=（2，3），

    ∴k–=k（1，–5）–（2，3）=（k，–5k）–（2，3）=（k–2，–5k–3），

    又+3=（1，–5）+3（2，3）=（1，–5）+（6，9）=（7，4），

    且k–与+3平行，

    ∴7（–5k–3）–4（k–2）=0，解得k=–．

    ∴实数k的值为–．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四面体中，分别是线段的中点，，，，直线与平面所成的角等于．

    （Ⅰ）证明：平面平面；

    （Ⅱ）求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市有一特色酒店由一些完全相同的帐篷构成.每座帐篷的体积为立方米，且分上下两层，其中上层是半径为（单位：米）的半球体，下层是半径为米，高为米的圆柱体（如图）.经测算，上层半球体部分每平方米建造费用为2千元，下方圆柱体的侧面、隔层和地面三个部分平均每平方米建造费用为3千元，设每座帐篷的建造费用为千元.

    参考公式：球的体积，球的表面积，其中为球的半径.

    （1）求关于的函数解析式，并指出该函数的定义域；

    （2）当半径为何值时，每座帐篷的建造费用最小，并求出最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂每月生产一种投影仪的固定成本为万元，但每生产台，需要加可变成本（即另增加投入）万元，市场对此产品的月需求量为台，销售的收入函数为（万元）且，其中是产品售出的数量（单位：百台）．

    (1)求月销售利润（万元）关于月产量(百台)的函数解析式；

    (2)当月产量为多少时，销售利润可达到最大？最大利润为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】三角形面积为S=(a+b+c)r,a,b,c为三角形三边长,r为三角形内切圆半径,利用类比推理,可以得出四面体的体积为 ( )

    A. V=abc B. V=Sh

    C. V=(ab+bc+ac)·h(h为四面体的高) D. V=(S1+S2+S3+S4)·r(其中S1,S2,S3,S4分别为四面体四个面的面积,r为四面体内切球的半径,设四面体的内切球的球心为O,则球心O到四个面的距离都是r)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知椭圆的离心率为， ， 分别为椭圆的上顶点和右焦点， 的面积为，直线与椭圆交于另一个点，线段的中点为.

    （1）求直线的斜率；

    （2）设平行于的直线与椭圆交于不同的两点， ，且与直线交于点，求证：存在常数，使得.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高校共有学生15 000人，其中男生10 500人，女生4500人．为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据(单位：小时)．

    (1)应收集多少位女生的样本数据？

    (2)根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图(如图所示)，其中样本数据的分组区间为：[0，2]，(2，4]，(4，6]，(6，8]，(8，10]，(10，12]．估计该校学生每周平均体育运动时间超过4小时的概率．

    (3)在样本数据中，有60位女生的每周平均体育运动时间超过4小时，请完成每周平均体育运动时间与性别列联表，并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“搜索指数”是网民通过搜索引擎，以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大，表示网民对该关键词的搜索次数越多，对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中，某个关键词的搜索指数变化的走势图.

    根据该走势图，下列结论正确的是（ ）

    A. 这半年中，网民对该关键词相关的信息关注度呈周期性变化

    B. 这半年中，网民对该关键词相关的信息关注度不断减弱

    C. 从网民对该关键词的搜索指数来看，去年10月份的方差小于11月份的方差

    D. 从网民对该关键词的搜索指数来看，去年12月份的平均值大于今年1月份的平均值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭园C： +=1(a>b>0)的左、右焦点分别为F1，F2.且椭圆C过点(，-)，离心率e=;点P在椭圆C 上，延长PF1与椭圆C交于点Q,点R是PF2中点.

    (I )求椭圆C的方程;

    (II )若O是坐标原点，记△QF1O与△PF1R的面积之和为S,求S的最大值。

    查看答案和解析>>

    同步练习册答案