
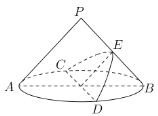
【题目】我们知道:用平行于圆锥母线的平面(不过顶点)截圆锥,则平面与圆锥侧面的交线是抛物线一部分,如图,在底面半径和高均为2的圆锥中,![]()
![]() 是底面圆
是底面圆![]() 的两条互相垂直的直径,
的两条互相垂直的直径,![]() 是母线
是母线![]() 的中点,已知过
的中点,已知过![]() 与
与![]() 的平面与圆锥侧面的交线是以
的平面与圆锥侧面的交线是以![]() 为顶点的圆锥曲线的一部分,则该圆锥曲线的焦点到其准线的距离等于__________.
为顶点的圆锥曲线的一部分,则该圆锥曲线的焦点到其准线的距离等于__________.
科目:高中数学 来源: 题型:
【题目】随着6月6日![]() 商用牌照发放,中国正式进入
商用牌照发放,中国正式进入![]() 商用时代.某人在一山坡
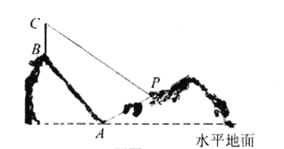
商用时代.某人在一山坡![]() 处观测对面山顶上的一座
处观测对面山顶上的一座![]() 基站(如图),图中所示的山坡均可视为直线,其中基站所在的山坡
基站(如图),图中所示的山坡均可视为直线,其中基站所在的山坡![]() 的坡角为
的坡角为![]() ,点
,点![]() 所在山坡
所在山坡![]() 的坡度为
的坡度为![]() .基站点
.基站点![]() 距坡谷点
距坡谷点![]() 的距离为
的距离为![]() 米,点
米,点![]() 距坡谷点
距坡谷点![]() 的距离为
的距离为![]() 米,且在点
米,且在点![]() 处测得塔顶点
处测得塔顶点![]() 的仰角是
的仰角是![]() .求基站
.求基站![]() 的高度.(参考数据:
的高度.(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左顶点
,左顶点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若以
两点,若以![]() 为直径的圆经过坐标原点,证明:
为直径的圆经过坐标原点,证明:![]() 到直线
到直线![]() 的距离为定值.
的距离为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cosxsin(x+![]() )-1.
)-1.
(1)求f(x)的最小正周期和单调递减区间;
(2)将y=f(x)图象上所有的点向右平行移动![]() 个单位长度,得到y=g(x)的图象.若g(x)在(0,m)内是单调函数,求实数m的最大值.
个单位长度,得到y=g(x)的图象.若g(x)在(0,m)内是单调函数,求实数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲,乙两地某月![]() 时的气温,随机选取该月中的
时的气温,随机选取该月中的![]() 天,将这
天,将这![]() 天中
天中![]() 时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:①甲地该月
时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:①甲地该月![]() 时的平均气温低于乙地该月
时的平均气温低于乙地该月![]() 时的平均气温;②甲地该月
时的平均气温;②甲地该月![]() 时的平均气温高于乙地该月
时的平均气温高于乙地该月![]() 时的平均气温;③甲地该月
时的平均气温;③甲地该月![]() 时的气温的中位数小于乙地该月
时的气温的中位数小于乙地该月![]() 时的气温的中位数;④甲地该月
时的气温的中位数;④甲地该月![]() 时的气温的中位数大于乙地该月
时的气温的中位数大于乙地该月![]() 时的气温的中位数.其中根据茎叶图能得到的正确结论的编号为( )
时的气温的中位数.其中根据茎叶图能得到的正确结论的编号为( )

A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个工厂生产某种产品每年需要固定投资100万元,此外每生产1件该产品还需要增加投资1万元,年产量为![]() (
(![]() )件.当
)件.当![]() 时,年销售总收人为(
时,年销售总收人为(![]() )万元;当
)万元;当![]() 时,年销售总收人为
时,年销售总收人为![]() 万元.记该工厂生产并销售这种产品所得的年利润为
万元.记该工厂生产并销售这种产品所得的年利润为![]() 万元.(年利润=年销售总收入一年总投资)
万元.(年利润=年销售总收入一年总投资)
(1)求![]() (万元)与
(万元)与![]() (件)的函数关系式;
(件)的函数关系式;
(2)当该工厂的年产量为多少件时,所得年利润最大?最大年利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某贫困地区有1500户居民,其中平原地区1050户,山区450户.为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据(单位:万元).
(Ⅰ)应收集多少户山区家庭的样本数据?
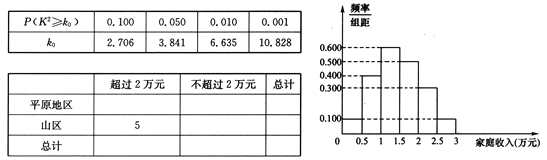
(Ⅱ)根据这150个样本数据,得到2017年家庭收入的频率分布直方图(如图所示),其中样本数据分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
.如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
(Ⅲ)样本数据中,由5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有![]() 的把握认为“该地区2017年家庭年收入与地区有关”?
的把握认为“该地区2017年家庭年收入与地区有关”?
附:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com