
分析 根据平面向量的运算性质计算.
解答 解:(1))$\overrightarrow{a}$•$\overrightarrow{b}$=x1x2+y1y2;
(2)|$\overrightarrow{a}$|=$\sqrt{\overrightarrow{a}•\overrightarrow{a}}$=$\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}$;
(3)$\overrightarrow{a}$⊥$\overrightarrow{b}$?$\overrightarrow{a}•\overrightarrow{b}=0$?x1x2+y1y2=0;
(4)cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{{x}_{1}{x}_{2}+{y}_{1}{y}_{2}}{\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}\sqrt{{{x}_{2}}^{2}+{{y}_{2}}^{2}}}$.
故答案为:(1)x1x2+y1y2;(2)$\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}$;(3)$\overrightarrow{a}•\overrightarrow{b}=0$,x1x2+y1y2=0;(4)$\frac{{x}_{1}{x}_{2}+{y}_{1}{y}_{2}}{\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}\sqrt{{{x}_{2}}^{2}+{{y}_{2}}^{2}}}$.
点评 本题考查了平面向量的数量积运算的性质,属于基础题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:高中数学 来源: 题型:解答题
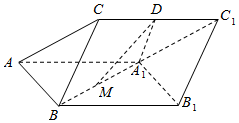 如图,三棱柱ABC-A1B1C1中,D,M分别为CC1,A1B的中点,A1D⊥CC1,△AA1B是边长为2的正三角形,A1D=2,BC=1.
如图,三棱柱ABC-A1B1C1中,D,M分别为CC1,A1B的中点,A1D⊥CC1,△AA1B是边长为2的正三角形,A1D=2,BC=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若b∥a,则b∥α | B. | 若b⊥α,则b⊥a | C. | 若b∥α,则b∥a | D. | 若b⊥a,则b⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{12\sqrt{13}}{13}$ | D. | $\frac{28\sqrt{13}}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com