
分析 根据古典概型的概率公式求出三种球的个数,再计算ξ=0,1,2时的概率,得出数学期望.
解答 解:设黑球,白球,红球个数分别是x,y,z,则
$\left\{\begin{array}{l}{x+y+z=15}\\{\frac{x}{15}=\frac{2}{5}}\\{\frac{{C}_{y}^{2}}{{C}_{15}^{2}}=\frac{2}{21}}\end{array}\right.$,解的x=6,y=5,z=4.
ξ的可能取值为0,1,2,
∴P(ξ=0)=$\frac{{C}_{11}^{2}}{{C}_{15}^{2}}$=$\frac{11}{21}$,P(ξ=1)=$\frac{{{C}_{4}^{1}C}_{11}^{1}}{{C}_{15}^{2}}$=$\frac{44}{105}$,P(ξ=2)=$\frac{{C}_{4}^{2}}{{C}_{15}^{2}}$=$\frac{2}{35}$,
∴Eξ=0×$\frac{11}{21}$+1×$\frac{44}{105}$+2×$\frac{2}{35}$=$\frac{8}{15}$.
故答案为:$\frac{8}{15}$.
点评 本题考查了古典概型的概率计算,组合数公式的应用,离散型随机变量的数学期望,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
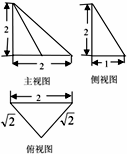
| A. | 1+$\sqrt{2}$+$\sqrt{3}$ | B. | 2+$\sqrt{2}$+$\sqrt{3}$ | C. | 3+$\sqrt{2}$+$\sqrt{3}$ | D. | 4+$\sqrt{2}$+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男 | 女 | 总计 | |
| 喜爱 | 40 | 60 | 100 |
| 不喜爱 | 20 | 20 | 40 |
| 总计 | 60 | 80 | 140 |
| p(k2≥k0 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.705 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1+a3>0 | B. | a1a3>0 | C. | S1+S3<0 | D. | S1S3<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com