
分析 (1)利用f(x)=g(x)+h(x)和f(-x)=g(-x)+h(-x)求出g(x)和h(x)的表达式,再求出p(t)关于t的表达式即可.
(2)先有x∈[1,2]找出t的范围,在把所求问题转化为求p(t)在[$\frac{3}{2}$,$\frac{15}{4}$]的最小值.让大于等于m2-m-1即可.
(3)转化为关于p(t)的一元二次方程,利用判别式的取值,再分别讨论即可.
解答 解:(1)假设f(x)=g(x)+h(x)①,其中g(x)偶函数,h(x)为奇函数,
则有f(-x)=g(-x)+h(-x),即f(-x)=g(x)-h(x)②,
由①②解得g(x)=$\frac{f(x)+f(-x)}{2}$,h(x)=$\frac{f(x)-f(-x)}{2}$,
∵f(x)定义在R上,∴g(x),h(x)都定义在R上.
∵g(-x)=$\frac{f(-x)+f(x)}{2}$=g(x),h(-x)=$\frac{f(-x)-f(x)}{2}$=-h(x).
∴g(x)是偶函数,h(x)是奇函数,∵f(x)=2x+1,
∴g(x)=$\frac{f(x)+f(-x)}{2}$=$\frac{2x+1+2-x+1}{2}$=2x+$\frac{1}{2x}$,
h(x)=$\frac{f(x)-f(-x)}{2}$=$\frac{2x+1-2-x+1}{x}$=2x-$\frac{1}{2x}$,
由2x-$\frac{1}{2x}$=t,则t∈R,
平方得t2=(2x-$\frac{1}{2x}$)2=22x+$\frac{1}{{2}^{2x}}$-2,∴g(2x)=22x+$\frac{1}{{2}^{2x}}$=t2+2,
∴p(t)=t2+2mt+m2-m+1.
(2)∵t=h(x)关于x∈[1,2]单调递增,
∴$\frac{3}{2}$≤t≤$\frac{15}{4}$,
∴p(t)=t2+2mt+m2-m+1≥m2-m-1对于t∈[$\frac{3}{2}$,$\frac{15}{4}$]恒成立,
∴m≥-$\frac{{t}^{2}+2}{2t}$对于t∈[$\frac{3}{2}$,$\frac{15}{4}$]恒成立,
令φ(t)=-$\frac{{t}^{2}+2}{2t}$,则φ′(t)=$\frac{1}{2}$($\frac{2}{{t}^{2}}$-1),
∵t∈[$\frac{3}{2}$,$\frac{15}{4}$],∴φ′(t)=$\frac{1}{2}$($\frac{2}{{t}^{2}}$-1)<0,
故φ(t)在t∈[$\frac{3}{2}$,$\frac{15}{4}$]上单调递减,
∴φ(t)max=φ($\frac{3}{2}$)=-$\frac{17}{12}$,
∴m≥-$\frac{17}{12}$.
(3)由(1)得p(p(t))=[p(t)]2+2mp(t)+m2-m+1,
若p(p(t))=0无实根,即[p(t)]2+2mp(t)+m2-m+1①无实根,
方程①的判别式△=4m2-4(m2-m+1)=4(m-1).
1°当方程①的判别式△<0,即m<1时,方程①无实根.
2°当方程①的判别式△≥0,即m≥1时,
方程①有两个实根p(t)=t2+2mt+m2-m+1=-m±$\sqrt{m-1}$,
即t2+2mt+m2+1±$\sqrt{m-1}$=0②,
只要方程②无实根,故其判别式△2=4m2-4(m2+1±$\sqrt{m-1}$)<0,
即得-1-$\sqrt{m-1}$<0③,且-1+$\sqrt{m-1}$<0④,
∵m≥1,③恒成立,由④解得m<2,∴③④同时成立得1≤m<2.
综上,m的取值范围为m<2.
点评 本题是在考查指数函数的基础上对函数的恒成立问题,函数奇偶性以及一元二次方程根的判断的综合考查,是一道综合性很强的难题.


科目:高中数学 来源: 题型:填空题
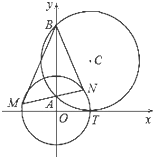 如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(在A的上方),且|AB|=2.过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:
如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(在A的上方),且|AB|=2.过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | (-∞,-1) | C. | (-∞,0] | D. | (-∞,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<m<1 | B. | -4<m<2 | C. | m<1 | D. | -3<m<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 1或-3 | D. | 3或-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{42}{125}$ | B. | $\frac{18}{125}$ | C. | $\frac{6}{25}$ | D. | $\frac{12}{125}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com