
分析 (1)根据函数有意义,分母不能为零,即可得到的取值范围
(2)采用分离常数法,根据定义域范围求解值域.
解答 解:(1)∵函数y=$\frac{x+2}{3x-4}$.
∴3x-4≠0
解得:$x≠\frac{4}{3}$
故x的取值范围是{x∈R|$x≠\frac{4}{3}$}.
(2)函数y=$\frac{x+2}{3x-4}$
化简成:y=$\frac{\frac{1}{3}(3x-4)+\frac{4}{3}+2}{3x-4}$=$\frac{\frac{1}{3}(3x-4)+\frac{10}{3}}{3x-4}$=$\frac{1}{3}+\frac{10}{9x-12}$
∵$\frac{10}{9x-12}≠0$
∴y≠$\frac{1}{3}$
故y的取值范围是{y∈R|$y≠\frac{1}{3}$}.
点评 本题考查了函数的定义域和值域的求法,分离常数法是求值域的方法之一,必须熟悉并且要灵活运用.属于基础题.


科目:高中数学 来源: 题型:解答题
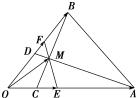 在△OAB中,$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$,$\overrightarrow{OD}$=$\frac{2}{5}$$\overrightarrow{OB}$,AD与BC交于点M,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$.在线段AC上取一点E,在线段BD上取一点F,使EF过点M,设$\overrightarrow{OE}$=p$\overrightarrow{OA}$,$\overrightarrow{OF}$=q$\overrightarrow{OB}$.
在△OAB中,$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$,$\overrightarrow{OD}$=$\frac{2}{5}$$\overrightarrow{OB}$,AD与BC交于点M,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$.在线段AC上取一点E,在线段BD上取一点F,使EF过点M,设$\overrightarrow{OE}$=p$\overrightarrow{OA}$,$\overrightarrow{OF}$=q$\overrightarrow{OB}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男 | 女 | 总计 | |
| 喜爱 | 40 | 60 | 100 |
| 不喜爱 | 20 | 20 | 40 |
| 总计 | 60 | 80 | 140 |
| p(k2≥k0 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.705 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(b)<f(a)<f(c) | B. | f(c)<f(b)<f(a) | C. | f(c)<f(a)<f(b) | D. | f(b)<f(c)<f(a) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com