练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．已知向量$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（1，-1），则2$\overrightarrow{a}$+$\overrightarrow{b}$=（　　）
    A．10B．（5，5）C．（5，6）D．（5，7）

    分析 根据题意，由向量$\overrightarrow{a}$、$\overrightarrow{b}$的坐标，结合向量坐标运算的法则，可得2$\overrightarrow{a}$+$\overrightarrow{b}$=2（2，3）+（1，-1），计算即可得答案．

    解答 解：根据题意，向量$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（1，-1），
    则2$\overrightarrow{a}$+$\overrightarrow{b}$=2（2，3）+（1，-1）=（5，5）；
    即2$\overrightarrow{a}$+$\overrightarrow{b}$=（5，5）；
    故选：B．

    点评 本题考查向量的坐标运算，注意向量的表示形式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．如果$\sqrt{x+\sqrt{2}}$+|y-1|=0，则|$\frac{1}{x+y}$|=（　　）
    A．1-$\sqrt{2}$B．1+$\sqrt{2}$C．$\sqrt{2}$-1D．-$\sqrt{2}$-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知cosα=$\frac{3}{5}$，cosβ=$\frac{\sqrt{2}}{2}$，且α，β∈（0，$\frac{π}{2}$），求tan2（α-β）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．从点A（1，-1，3）沿向量$\overrightarrow{a}$=（2，1，-1）的方向取长为2$\sqrt{6}$的线段AB，则点B的坐标为（5，1，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知函数f（x）=2x2-1，f（a）=7，则a=±2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知椭圆：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，且经过点（-$\sqrt{3}$，$\frac{1}{2}$）．
    （1）求椭圆C的方程；
    （2）点P是椭圆C上任一点，以P为圆心，|OP|的长为半径的圆P与圆F：（x-$\sqrt{3}$）2+y2=5（F是圆心）的一个公共点为Q．证明：点Q到直线PF的距离为定值，并求此值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

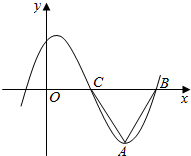    8．已知向量$\overrightarrow{a}$=（2cos$\frac{ωx}{2}$，$\sqrt{3}$），$\overrightarrow{b}$=（3cos$\frac{ωx}{2}$，sinωx），ω＞0，设函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$-3的部分图象如图所示，A为图象的最低点，B，C为图象与x轴的交点，且△ABC为等边三角形，其高为2$\sqrt{3}$．
    （Ⅰ）求ω的值及函数f（x）的值域；
    （Ⅱ）若f（x0）=$\frac{8\sqrt{3}}{5}$，且x0∈（-$\frac{10}{3}$，$\frac{2}{3}$ ），求f（x0+1）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

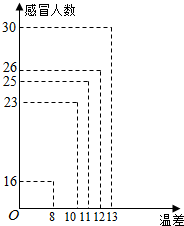    4．近五天某市气温变化异常，昼夜温差越来越大，感冒的学生较多，该市某校教学兴趣小组从气象站与校医室分别收集了近五天的昼夜温差大小与患感冒人数的数据，得到了如下的散点图：该兴趣小组确定的研究方案是：先从这五组数据中选取两组，用剩下的三组数据求线性回归方程，再对被选取的两组数据进行险验．
    （1）求选取的两组数据恰好是不相邻两天数据的概率；
    （2）若选取的是温差为8度与10度的两组数据，请根据其余三组数据，求出感冒人数y关于温差x的线性回归方程．

    查看答案和解析>>

    科目：高中数学 来源：2017届湖北襄阳四中高三七月周考三数学（理）试卷（解析版） 题型：解答题

    选修4-5：不等式选讲

    设函数．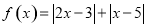

    （1）求不等式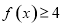的解集；

    （2）若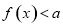的解集不是空集，求实数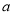的取值范围．

    查看答案和解析>>

    同步练习册答案