
分析 题目要求解的是两条异面直线所成角的,通过寻找平行线,BC1∥AD1,异面直线AD1与BD所成的角为∠DBC1,△DBC1是等边三角形,可得∠DBC1的大小.给出了AB的中点为M,DD1的中点为N,过M点作CN平形线交AA1于F,连接MF,得到异面直线B1M与CN所成的角为∠FMB1,求出三条边的长度,满足勾股定理,即可求∠FMB1的大小.
解答 解:由题意:ABCD-A1B1C1D1是正方体,BC1∥AD1,
异面直线AD1与BD所成的角为∠DBC1,连接C1D,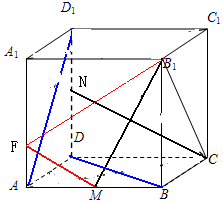 可得:DB,C1D,BC1是正方形的对角线,
可得:DB,C1D,BC1是正方形的对角线,
∴DB=C1D=BC1
所以△DBC1是等边三角形,
异面直线AD1与BD所成的角为∠DBC1=60°.
AB的中点为M,DD1的中点为N,
过M点作CN平形线交AA1于F,连接MF,
异面直线B1M与CN所成的角为∠FMB1,
设正方体的边长为a,则CN=MB1=$\frac{\sqrt{5}}{2}a$,
MF=$\frac{1}{2}$CN=$\frac{\sqrt{5}}{4}a$,B1F=$\sqrt{{A}_{1}{{B}_{1}}^{2}+{A}_{1}{F}^{2}}=\sqrt{{a}^{2}+\frac{9}{16}{a}^{2}}=\frac{5}{4}a$.
∵$M{F}^{2}+M{{B}_{1}}^{2}=F{{B}_{1}}^{2}$.
∴FM⊥MB1
即异面直线B1M与CN所成的角为90°.
故答案为:60°,90°.
点评 本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧,此题是中低档题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8个 | B. | 7个 | C. | 6个 | D. | 5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 内切 | B. | 外切 | C. | 相交 | D. | 外离 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {1,2} | C. | {2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0.50 | 0.99 | 2.01 | 3.98 |
| y | -0.99 | 0.01 | 0.98 | 2.00 |
| A. | y=2x | B. | y=x2-1 | C. | y=log2x | D. | y=2x-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,+∞) | C. | (-9,+∞) | D. | (-∞,-9) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 6 | C. | 4 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com