
已知函数 ,函数g(x)的导函数
,函数g(x)的导函数 ,且
,且
(1)求 的极值;
的极值;
(2)若 ,使得
,使得 成立,试求实数m的取值范围:
成立,试求实数m的取值范围:
(3)当a=0时,对于 ,求证:
,求证:
(1)当a≥0时,  没有极值;当a<0时,
没有极值;当a<0时, 取得极大值
取得极大值 =
= ;(2)
;(2)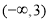 ;(3)见解析.
;(3)见解析.
【解析】
试题分析:(1)求函数定义域、导数,按照a≥0,a<0两种情况讨论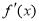 的符号变化,由极值定义可求得
的符号变化,由极值定义可求得 的极值;(2)先由条件求出
的极值;(2)先由条件求出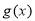 ,存在x∈(0,+∞),使得
,存在x∈(0,+∞),使得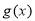 <
< 成立,即m<
成立,即m< 成立.令
成立.令 =
= ,x∈(0,+∞),则问题等价于m<
,x∈(0,+∞),则问题等价于m<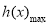 ,利用基本不等式可判定导数研究
,利用基本不等式可判定导数研究 的正负时,从而判定出函数
的正负时,从而判定出函数 的单调性,从而可求得
的单调性,从而可求得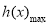 ;(3)当a=0时,先将
;(3)当a=0时,先将 具体化为
具体化为 ,令
,令 =
= =
= ,利用导数通过研究
,利用导数通过研究 的单调性、极值,从而得出函数
的单调性、极值,从而得出函数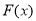 的图像性质,求出
的图像性质,求出 的最小值,只要证明最小值大于零即证明了
的最小值,只要证明最小值大于零即证明了 .
.
试题解析: (1)函数 的定义域为(0,+∞),
的定义域为(0,+∞), =
=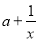 (
( >0).
>0).
(i)当a≥0时, >0,
>0,
函数 在(0,+∞)上单调递增,故
在(0,+∞)上单调递增,故 没有极值;
没有极值;
(ii)当a<0时, =
=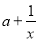 =
= ,
,
当x∈(0,﹣ )时,
)时, >0;当x∈(﹣
>0;当x∈(﹣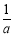 ,+∞)时,
,+∞)时, <0,
<0,
∴当x=﹣ 时,
时, 取得极大值
取得极大值 =
= .
.
(2)∵函数 的导函数
的导函数 =
= ,
,
∴ =
= +c(其中c为常数)
+c(其中c为常数)
由 ,得(1+c)e=e,故c=0,
,得(1+c)e=e,故c=0,
∴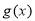 =
= .
.
若存在x∈(0,+∞),使得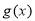 <
< 成立,即m<
成立,即m< 成立.
成立.
令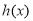 =
= ,x∈(0,+∞),则问题等价于m<
,x∈(0,+∞),则问题等价于m<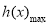 ,
,
∴ =1﹣
=1﹣ ,
,
∵当x∈(0,+∞)时, >1,
>1, ≥
≥ =
=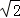 ,
,
∴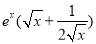 >1,故
>1,故 <0,
<0,
∴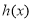 在(0,+∞)上单调递减,
在(0,+∞)上单调递减,
∴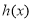 <
< =3,故m<3.
=3,故m<3.
(3)解:当a=0时, =lnx,
=lnx,
令 =
= ﹣
﹣ ﹣2=
﹣2= ﹣lnx﹣2,
﹣lnx﹣2,
 =
= ,而
,而 =
= >0在(0,+∞)上恒成立,
>0在(0,+∞)上恒成立,
∴ 在(0,+∞)上单调递增.
在(0,+∞)上单调递增.
设 =0的根为x=t,则
=0的根为x=t,则 ,即t=
,即t= .
.
当x∈(0,t)时, <0,则
<0,则 在(0,t)上单调递减;
在(0,t)上单调递减;
当x∈(t,+∞)时, >0,则
>0,则 在(t,+∞)上单调递增.
在(t,+∞)上单调递增.
故 min=
min= =
= =
= =
= .
.
由 =e﹣1>0,
=e﹣1>0, =
= ﹣2<0,得t∈
﹣2<0,得t∈ ,
,
∵ =
= 在(
在( ,1)上单调递增,
,1)上单调递增,
∴ min=
min= >
> =
= +
+ ﹣2>
﹣2>
 ﹣2=0.
﹣2=0.
∴ ﹣
﹣ >2.
>2.
考点: 导数在最大值、最小值问题中的应用;利用导数研究函数的极值


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2015届江西省九江市七校高二下学期期中联考文科数学试卷(解析版) 题型:选择题
已知图①中的图像对应的函数为 ,则图②的图像对应的函数为( )
,则图②的图像对应的函数为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
已知二次函数 的导函数为
的导函数为 ,且
,且 >0,
>0, 的图象与x
的图象与x
轴恰有一个交点,则 的最小值为 ( )
的最小值为 ( )
A.3 B. C.2 D.
C.2 D.
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
设 是关于t的方程
是关于t的方程 的两个不等实根,则过
的两个不等实根,则过 ,
, 两点的直线与双曲线
两点的直线与双曲线 的公共点的个数为
的公共点的个数为
A.3 B.2 C.1 D.0
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
某校夏令营有3名男同学 和3名女同学
和3名女同学 ,其年级情况如下表:
,其年级情况如下表:
| 一年级 | 二年级 | 三年级 |
男同学 |
|
|
|
女同学 |
|
|
|
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同)
(1)用表中字母列举出所有可能的结果
(2)设 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源:2015届江西省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
抛物线 :
: 的焦点与双曲线
的焦点与双曲线 :
: 的右焦点的连线交
的右焦点的连线交 于第一象限的点
于第一象限的点 ,若
,若 在点
在点 处的切线平行于
处的切线平行于 的一条渐近线,则
的一条渐近线,则 ( )
( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届江西省上饶市高二下学期期末考试理科数学试卷(解析版) 题型:填空题
观察下列等式23=3+5,33=7+9+11,43=13+15+17+19,53=21+23+25+27+29, ,若类似上面各式方法将m3分拆得到的等式右边最后一个数是131,则正整数m等于 _________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com