Question

【题目】在平面直角坐标系xOy中，直线l的参数方程为 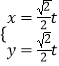（t为参数），圆C的方程为x2+y2﹣4x﹣2y+4=0．以O为极点，x轴正半轴为极轴建立极坐标系．
（1）求l的普通方程与C的极坐标方程；
（2）已知l与C交于P，Q，求|PQ|．

Answer 1

【答案】
（1）解：圆C的方程为x2+y2﹣4x﹣2y+4=0．

曲线C的标准方程为（x﹣2）2+（y﹣1）2=1．

把x=ρcosθ，y=ρsinθ代入，化简得：曲线C的极坐标方程为：ρ2﹣4ρcosθ﹣2sinθ+4=0

（2）解：将直线l的参数方程 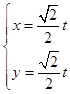（t为参数），代入曲线C的方程，得t2﹣3 t+4=0，

t1+t2=3 ，t1t2=4，

∴|PQ|=|t1﹣t2|= = =

【解析】（1）圆C的方程为x2+y2﹣4x﹣2y+4=0．曲线C的标准方程为（x﹣2）2+（y﹣1）2=1．把x=ρcosθ，y=ρsinθ代入，化简得：曲线C的极坐标方程．（2）将直线l的参数方程 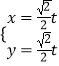（t为参数），代入曲线C的方程，得t2﹣3 t+4=0，利用|PQ|=|t1﹣t2|= 即可得出．